기업지배구조가 주식가격 결정의 효율성에 미치는 영향에 관한 연구*
The Effects of Corporate Governance on Stock Pricing Efficiency in the Korean Stock Market*
Article information
Abstract
본 연구는 기업지배구조가 좋을수록 과연 주식가격결정의 효율성이 향상되는지 실증적으로 규명 하고 있다. 주식가격결정의 효율성 측정을 위한 대용변수로서, 분산비율(variance ratio), Hou and Moskowits(2005)이 제안한 가격결정 비효율성 지표, Hurst 지수(Hurst, 1951)를 종속변수로 사용 한다. 실증분석 결과, 기업지배구조가 우수할수록 분산비율(variance ratio)은 더욱 1에 접근하였고, 가격결정의 지연 정도는 감소하였으며, Hurst 지수는 random walk을 나타내는 0.5 값에 더욱 근접 하였다. 끝으로, 강건성 분석을 위해 고유위험(idiosyncratic volatility), 왜도(skewness)를 종속변수로 사용한 패널분석 결과, 기업지배구조가 양호할수록 고유위험이 감소하여 주가의 안정성이 증가되었고, 왜도가 감소하여 복권성향(lottery)의 투자가 감소하였다. 한편, 이처럼 좋은 기업지배구조가 주식가격 결정에 미치는 긍정적인 영향은, 특히 “주주권리보호”가 잘되어 있는 경우에 더욱 성립하였다. 이러한 결과들은 기존의 좋은 기업지배구조의 필요성을 주장하는 일련의 연구들과 맥을 같이 한다.
Trans Abstract
This study investigates whether better corporate governance enhances the efficiency of stock pricing in the Korean stock market. The variance ratio (Lo and MacKinlay, 1988) is set as a proxy variable for the efficiency of stock pricing. Moreover, the degree of delayed stock pricing (Hou and Moskowits, 2005) is used as a proxy for the inefficiency of stock pricing. In addition, another measure of delayed stock pricing (Hou and Moskowits, 2005) is used as an additional proxy. Moreover, the Hurst Index, representative of the efficiency of stock pricing, is also used. According to the empirical investigation, better corporate governance drives the variance ratio to one (unity), reduces the degree of delay in stock pricing, and leads to a Hurst Index of 0.5, which represents the random walk process of the stock returns. Finally, for robustness checks, idiosyncratic volatility and skewness are set as dependent variables. The empirical results show that better governance reduces the idiosyncratic volatility and the skewness of individual stock returns. These findings indicate that better corporate governance enhances stock pricing efficiency. These results are therefore linked to the previous literature that argues that good governance should be set up necessarily.
1. 서론
본 연구는 기업지배구조가 좋을수록 주식가격결정의 효율성이 증가되는지 실증분석 한다. 이 때 분석대상 기업은 KOSPI 기업으로 한정한다. 기업지배구조에 대한 일련의 연구들에 의하면, 지배구조가 우수할수록 기업의 투명성이 향상되어 정보비대칭 현상이 현저히 감소한다. 만일 기업과 투자자간 정보비대칭 정도가 낮다면 이는 주식가격 결정에 긍정적인 영향을 줄 수 있을 것이다.
한편, 주식가격결정의 효율성은 Lo and MacKinlay(1988) 이후 흔히 분산비율(variance ratio)로써 측정하되, 이 값이 1에 가까울수록 가격결정의 효율성이 높다고 판단한다. 또한 Hou and Moskowits(2005)이 제안한 가격결정 비효율성 지표(가격발견의 지연 정도) 역시 주식가격 결정의 효율성을 측정하는 중요한 도구로 인식되고 있다. 즉, 가격발견 지연 정도가 작을수록 주식가격이 더욱 효율적으로 형성되는 것으로 해석한다. 그리고 Hurst 지수(Hurst, 1951)는 그 값이 0.5에 가까울수록 랜덤워크를 따르는 것으로 알려져 있다.
본 연구는 상기 두 가지 현상을 연결하여 그 인과관계를 밝히는 논문이다. 본 논문은 기업지배구조가 가격결정의 효율성에 어떠한 영향을 주는지 아직까지 연구된 바가 없다는 점에서 연구의 의의가 있다. 또한 만일 지배구조가 취약할수록 주식가격결정의 효율성을 더욱 저해한다면, 이는 국내 주식시장을 교란하는 중요한 요인이 개별기업의 지배구조라는 점에서 정책 당국의 개입이 요구됨을 시사한다.
기업-연도 고정효과 패널분석 및 Newey and West(1987) 표준오차를 사용한 실증분석 결과, 변동성 군집효과(volatility clustering)의 고려여부와 관계없이 일관되게 기업지배구조가 우수 할수록 분산비율(variance ratio)은 공히 더욱 1에 근접하였다. 또한 개별기업 주가수익률의 과거값(lag) 및 미래값(lead)을 모형에 포함하건 포함하지 않건, 기업지배구조가 양호할수록 Hou and Moskowits(2005)에 의한 가격결정의 지연 정도는 유의하게 감소함을 발견하였다. 그리고 기업지배구조가 우수할수록 Hurst 지수는 random walk을 나타내는 0.5 값에 더욱 근접하였다. 끝으로, 강건성 분석을 위해 고유위험(idiosyncratic volatility), 왜도(skewness)를 종속변수로 사용한 패널분석 결과, 기업지배구조가 양호할수록 고유위험이 감소하여 주가의 안정성이 증가되었고, 왜도가 감소하여 복권성향(lottery)의 투자가 감소하였다. 특히 이러한 실증결과들은 정보비대칭을 측정하는 대리변수인 1/평균거래량을 통제변수로 설정하여도 여전히 강건하였다.
이 때 왜도의 경우, 주가수익률의 평균과 중앙값이 1% 수준에서 유의한 양(+)의 값을 가졌던 바, 회귀분석 결과 기업지배구조가 우수할수록 이러한 왜도가 감소함으로써 주가 수익률이 정규분포에 보다 가까워졌다. 이러한 왜도의 감소는, 지배구조가 좋은 기업일수록 투자자는 복권성향(lottery)의 투자를 더욱 지양함을 시사하며, 이는 다시 주식시장의 안정성을 증진시키는 효과로 해석될 수 있다.
요컨대, 위의 실증결과는 좋은 기업지배구조가 주식가격 결정의 효율성을 더욱 향상시키는 것을 의미하는 바, 이는 기존의 좋은 기업지배구조의 필요성을 주장하는 일련의 연구들과 맥을 같이 한다.
한편, 선행연구와의 연속성과 더불어 본 논문은 다음과 같은 시사점을 제공한다.
첫째, 기업지배구조가 취약할수록 주식가격이 비효율적으로 결정된다면, 이는 주식시장을 교란시킬 수 있는 기업이 바로 지배구조가 좋지 않은 기업임을 의미하므로, 금융당국의 주식시장 개입이 어느 정도 타당성을 갖고 있음을 시사한다.
둘째, 차익거래를 시도하는 투자자의 관점에서 본다면, 기업지배구조가 좋을수록 주식 가격이 더욱 효율적으로 결정된다는 사실은 굿뉴스일 수 있다. 왜냐하면, 어떤 투자자가 기본적 분석 등을 통하여 특정 종목이 저평가 되어 있음을 발견하였을 때, 만일 해당 기업의 지배구조가 양호하다면, 저평가된 종목의 주가가 균형가격으로 상승할 것이라는 동 투자자의 신뢰가 예상대로 현실이 될 가능성이 더욱 높을 것이기 때문이다. 즉, 주식가격 결정의 효율성은 투자자의 합리적 기대를 충족시킴으로써 주식시장의 정보에 대한 투자자의 신뢰를 고취시킬 수 있는 것이다.
본 논문은 총 5장으로 구성되어 있다. 제 2장에서는 선행연구 및 기존의 관련 연구를 살펴보고 본 논문의 가설을 제시한다. 제 3장에서는 분석자료와 분석방법을 설명한 후, 기초통계량을 제시한다. 제 4장에서는 실증분석 결과를 제시한다. 제 5장에서는 본 연구의 결과를 요약하고 결론을 제시한다.
2. 선행연구
본 연구와 다소 관련된 국내 선행연구로서, 먼저 Park et al.(2009)은 기업지배구조가 우량 할수록 그렇지 않은 기업에 비하여 사후적으로도 더욱 높은 수익률을 기록함을 보고 하였다. 즉, 좋은 기업지배구조는 더 높은 기업가치를 유도한다는 주장이다.
또한 Byun et al.(2011)는 정보비대칭의 정도를 나타내는 대리변수(proxy)로서 허쉬만-허핀달 지수(HH Index)를 사용하여, 정보비대칭이 심한 산업에 속한 기업이라도 지배구조가 우량 할수록 해당 기업은 투자를 줄이고 배당 또는 자사주 재매입을 통하여 주주에게 부를 환원하는 방식으로 경영활동을 규율함을 발견하였다. 또한 반대의 경우, 즉 정보비대칭이 심각하지 않은 경우에는 지배구조가 좋을수록 동 기업은 배당 또는 자사재매입을 줄이고 대신 실물투자를 확대함으로써 기업가치를 증가 시킨다는 사실을 보고하였다. 이러한 실증 결과는, 설령 정보비대칭이 심한 산업에 속하여 있더라도, 좋은 기업지배구조 장치를 도입하여 실행한다면 주식시장에서는 해당 기업에 대하여 긍정적인 반응과 해석을 낳음을 시사하는 결과로 이해될 수 있다. 즉, 우수한 지배구조는 주식시장 내 투자자들에게 긍정적인 신호를 신속하게 보내는 기능을 갖추고 있는 것으로 해석될 수 있다.
한편, 본고에서 사용하는 종속변수 중 하나인 가격반응지연정도(delay measure)를 사용하여 정보기술의 발전이 주식시장의 가격적응 속도에 미치는 영향을 실증분석 한 연구가 존재 하였다. Park et al. (2013)가 그러한 연구인 바, 이들은 한국의 경우 정보통신 기술의 발전 으로 인하여 주식시장의 가격 반영속도가 더욱 증가하였음을 보고하였다.
다음으로, 해외 선행연구의 경우 Jung et al.(2013)는 개인투자자의 공매도가 허용된 시기에는 그렇지 않은 시기에 비하여 가격발견기능(price discovery)이 더욱 증진되었음을 보고하였는 바, 기존에 개인투자자는 noisy trader라는 선입견과는 정반대되는 결과를 발견한 바 있다.
Bharath et al.(2009)는 정보비대칭의 대리변수로서 거래량(trade volume) 사용하여 정보 비대칭이 심한 경우에만 자본조달우선순위이론(pecking order theory)이 성립함을 보였다. 이에 따라 본고에서도 정보비대칭에 대한 대리변수로서 거래량의 함수를 사용하도록 한다.
끝으로, Liorente et al.(2002)은 거래량(trade volume)의 증가는 곧 정보거래(informed trading)에 근거함을 보였다. 이에 따라 본고에서도 거래량이 클수록 정보비대칭이 완화 된다는 사실에 근거하여 정보비대칭의 대리변수로서 역시 거래량의 함수를 설정하기로 한다.
3. 가설의 설정
본 절에서는 논문의 실증적 가설들을 검토한다.
먼저, 기업지배구조가 우수할수록 주식가격 결정의 효율성이 증대된다면, Lo and MacKinlay(1988)가 밝힌 바와 같이, variance ratio가 1에 수렴할 것이다. 따라서 아래와 같이 가설 1을 설정한다.
가설 1: 기업지배구조가 양호할수록 variance ratio가 1에 수렴할 것이다.
위 가설 1을 검정하기 위하여, 세 가지 측정치로써 variance ratio가 1에 수렴하는 정도를 측정한다. 첫째, 먼저 [주별 주가수익률의 분산]/[5×일별 주가수익률의 분산] 에서 1을 뺀 후 절대값을 취한다. 주가가 random walk을 따르면 variance ratio가 1에 수렴하므로, variance ratio에서 1을 뺀 값은 0에 수렴할 것이다. 또한 절대값은 그 값이 0 이상이므로, 결국 상기 측정치 값이 작을수록 주가는 random walk을 따른다고 볼 수 있다. 둘째, 첫 번째와 비슷한 취지로 [월별 주가수익률의 분산]/[4×주별 주가수익률의 분산] 에서 1을 뺀 후 절대값을 취한다. 셋째, 역시 유사한 취지로 [월별 주가수익률의 분산]/[20×일별 주가수익률의 분산] 에서 1을 뺀 후 절대값을 취한다.
한편, 주가수익률의 변동성의 경우, 흔히 군집현상(volatility clustering)이 발견되는 바, 본고에서는 이를 통제한 분산비율을 계산하기 위해 GARCH(1,1) 모형으로부터 산출된 분산으로써 분산비율을 계산한다. 이로써 분산비율은 OLS 및 GARCH(1,1) 모형 등 두 모형에서 산출된 각기 다른 두 종속변수로 설정된다.
이러한 6 가지 척도를 각각 종속변수로 설정하고, 독립변수로 기업지배구조 점수 비중을 설정하여 회귀분석 한다. 만일 지배구조 점수 비중의 회귀계수가 유의한 음(-)의 값을 갖는다면, 가설 1이 성립함을 의미한다.
그리고 여기에 더하여, 본고에서는 역시 주식가격 결정의 효율성을 또 다른 방법으로 측정하기 위해, 임의보행(random walk)의 정도를 나타내는 Hurst 지수(Hurst, 1951)를 사용한다. Hurst 지수가 0.5에 가까울수록 해당 변수는 임의보행 하는 것으로 알려져 있다. 이에 본고의 가설 2를 설정한다.
가설 2: 기업지배구조가 좋을수록 Hurst 지수는 0.5에 접근할 것이다.
위 가설 2의 검정과 관련하여, 종속변수로서 Hurst 지수에서 0.5를 차감한 후 절대값을 취한 값(Distance_Hurst)j을 설정하고 독립변수로서 기업지배구조 점수 비중을 설정하여 회귀분석 한다. 만일 지배구조 점수 비중의 회귀계수가 유의한 음(-)의 값을 갖는다면, 가설 3이 성립함을 의미한다.
한편, Hou and Moskowits(2005)이 제안한 가격결정 비효율성 지표(가격발견의 지연 정도) 역시 주식가격 결정의 효율성을 측정하는 중요한 도구로 인식되고 있어, 본 논문에서는 동 지표를 또 다른 종속변수로 설정한다. 이 때 Hou and Moskowits(2005)이 제안한 방법을 그대로 사용하여 종속변수를 설정함과 동시에, 개별기업 주가수익률의 과거값(lag)을 본래의 모형에 추가하여 새로운 가격발견의 지연정도를 측정한다.
이에 가설 3을 설정하면 아래와 같다.
가설 3: 기업지배구조가 양호할수록 Hou and Moskowits(2005)이 제안한 가격결정 지연 정도는 감소할 것이다.
위 가설 3의 검정과 관련하여, 종속변수로서 가격결정 지연정도를 설정하고 독립변수로서 기업지배구조 점수 비중을 설정하여 회귀분석 한다. 만일 지배구조 점수 비중의 회귀계수가 유의한 음(-)의 값을 갖는다면, 가설 3이 성립함을 의미한다.
한편, 기업지배구조가 좋을수록 기업의 경영투명성(transparency)과 책임성(accountability)이 높을 것이다. 이 때 경영투명성이 높다면 기업의 성과나 가치에 관한 정보들에 잡음(noise)이 적을 것이므로 주가의 변동성이 줄어들 가능성이 있다. 또한 경영진의 의사결정이나 성과와 관련된 정보들의 신뢰성이 높다면 주식시장의 투자자가 이를 과대하게 또는 과소하게 해석하여 반응하는 정도가 줄어들 것이므로 주가변동성이 낮아질 것으로 예상할 수 있다. 더욱이, 고유위험은 사업위험(business risk)중 시장위험을 제외한 (또는 독립적인) 부분으로 측정 되는데, 기업지배구조의 주요한 역할 중 하나는 기업경영에서 발생할 수 있는 잠재적 위험 요인을 사전에 인지하고 대응하는 것이라는 점에서 우수한 지배구조는 사업위험 자체를 감소시키는 효과가 있다.
이에 아래와 같은 가설을 설정한다.
가설 4: 기업지배구조가 양호할수록 기업고유위험(idiosyncratic risk)은 감소할 것이다.
가설 3의 검정시 고유위험은 시장모형(market model)을 사용하여 산출된 결정계수 R2에 대하여, 1-R2로써 측정한다(Ferreira and Laux, 2007 등). 이 때 시장모형이란, 종속변수는 기업 수익률로, 독립변수는 코스피지수 수익률로 설정한 회귀분석 모형을 뜻한다.
그리고 고유위험은 일별 주가수익률에 대하여 각 종목, 매 사업연도마다 하나씩 산출한다. 만일 고유위험을 종속변수로 설정하고 기업지배구조 점수 비중을 독립변수로 설정하여 회귀분석 한 결과, 지배구조 점수 비중의 회귀계수가 유의한 음(-)의 값을 갖는다면 이는 가설 3이 성립함을 의미한다.
다음으로, 흔히 일별 주가수익률은 양(+)의 왜도를 갖는 것으로 알려져 있다. 이는 복권 당첨에 가까운 게임(lottery)을 하는 경우의 확률분포를 뜻한다. 만일 이러한 양의 왜도가 감소한다면, 이는 주식시장이 복권당첨 경기가 열리는 것 같은 역할이 약화되고, 자본조달 이라는 본래의 기능이 더욱 강화된다는 것을 시사한다. 이를 기업지배구조와 연결한다면, 지배구조가 좋을수록 정보투명성이 향상될 것인 바, 이는 정보 비대칭 하에서 발생할 수 있는 많은 빈도의 높은 수익률을 보이는 정도가 감소함을 시사한다. 따라서 기업지배구조가 좋을수록 왜도가 감소할 가능성이 크다. 만일 지배구조가 우량한 종목일수록 그 수익률의 왜도가 감소하는 패턴을 보일 경우 이를 주식시장 전체에 대하여 자본조달이라는 긍정적인 기능을 강화 시킨다고 해석할 수 있다. 만일 그렇다면 이는 주식시장을 교란하기 보다는 보다 안정적으로 본래의 기능을 촉진하는 것이 바로 좋은 기업지배구조의 역할이라 할 수 있다. 이에 가설 4를 설정한다.
가설 5: 기업지배구조가 좋을수록 일별 주가수익률의 왜도(skewness)는 감소할 것이다.
가설 4를 검정하기 위해 종속변수로서 주가수익률의 왜도를, 독립변수로서 기업지배구조 점수 비중을 설정하여 회귀분석 한다. 만일 기업지배구조 점수 비중의 회귀계수가 유의한 음(-)의 값을 갖는다면, 이는 가설 4가 성립하는 것으로 해석한다.
4. 분석자료 및 모형
4.1 표본
본 연구의 표본은 기업지배구조원에서 제공하는 기업지배구조 점수 산정이 시작된 2002년 회계연도부터 2017년 회계연도까지를 표본기간으로 설정하되, 12월 결산법인만 분석대상으로 삼았다. 이는 기업표본의 대부분이 12월 결산법인이기 때문이며, 동시에 12월이 결산월이 아닌 여타의 표본을 포함할 때의 발생하는 시차의 문제가 존재하기 때문이다. 즉, 12월 결산법인이 아닌 기업들을 제외할 경우의 이득이 포함할 경우의 이득보다 크다고 판단했기 때문이다.
한편, 본 연구를 위한 데이터는 기업-연도 불균형 패널자료로서, 이상치 등을 제외한 총 표본수는 9,459개이다.
본 연구를 위해 활용된 데이터베이스는 KIS-VALUE 이며, 결측치 보완 등 필요에 따라 금융감독원 전자공시시스템으로부터 자료를 수집하였다.
4.2 변수의 정의
본 연구에서의 주요 종속변수는 크게 다섯 가지 종류의 변수들이다.
첫째, 주식가격결정의 효율성을 측정하는 지표로서 variance ratio(Lo and MacKinlay, 1988)를 설정하였다.
구체적으로, Distance_Random1은 “1-variance ratio”에 절대값을 취한 값이되, 이 때 variance ratio는 (1개 사업연도간 주별수익률의 분산)/5×(1개 사업연도간 일별수익률의 분산)으로 계산되었다(Lo and MacKinlay, 1987). 1-varince ratio의 절대값을 취한 값이 0에 가까울수록, 즉 그 값이 작을수록 주가수익률은 random walk을 따른다고 볼 수 있다.
마찬가지로 Distance_Random2는 “1-variance ratio”에 절대값을 취한 값이되, (1개 사업연도간 월별수익률의 분산)/4×(1개 사업연도간 주별수익률의 분산)으로 계산되었다.
역시 동일하게, Distance_Random3는 “1-variance ratio”에 절대값을 취한 값이되, (1개 사업연도간 월별수익률의 분산)/20×(1개 사업연도간 일별수익률의 분산)으로 계산되었다.
한편, 주가수익률의 변동성의 경우, 흔히 군집현상(volatility clustering)이 발견되는 바, 본고에서는 이를 통제한 분산비율을 계산하기 위해 GARCH(1,1) 모형으로부터 산출된 분산 으로써 분산비율(variance ratio)을 계산한다. 이로써 분산비율은 OLS 및 GARCH(1,1) 모형 등 두 모형에서 산출된 각기 다른 6가지 종속변수로 설정된다.
구체적으로, Distance_Random4~ Distance_Random6은 모두 GARCH(1,1)을 적용한 후 분산을 사용하여 분산비율(variance ratio)을 계산한다. 이 때 variance ratio4는 (1개 사업연도간 주별수익률의 분산)/5×(1개 사업연도간 일별수익률의 분산)으로 계산되며, 1- varince ratio의 절대값을 취한 값이 0에 가까울수록, 즉 그 값이 작을수록 주가수익률은 random walk을 따른다고 볼 수 있다.
마찬가지로 Distance_Random5는 “1-variance ratio”에 절대값을 취한 값이되, (1개 사업연도간 월별수익률의 분산)/4×(1개 사업연도간 주별수익률의 분산)으로 계산한다.
역시 동일하게, Distance_Random6는 “1-variance ratio”에 절대값을 취한 값이되, (1개 사업연도간 월별수익률의 분산)/20×(1개 사업연도간 일별수익률의 분산)으로 계산된다.
둘째, Hou and Moskowits(2005)이 제안한 가격결정 비효율성 지표(가격발견의 지연 정도)를 또 다른 가격결정의 효율성을 측정하기 위하여 주된 종속변수로 설정하였다. 회귀 모형으로 표현하여 설명하면 아래와 같다.
이 때 Ri,t는 기업 i의 t시점 주가수익률을 뜻하며, RM,t는 t시점의 코스피 지수 수익률을 의미한다. 그리고 RM,t-j는 각각 t-1, t-2, t-3, t-4시점의 코스피 지수 수익률을 뜻한다. 만일 특정 종목의 주가가 시장정보를 즉시 반영한다면
본고에서는 위의 Delay 변수 값이 클수록 가격결정의 효율성이 낮고, 반대로 Delay가 작을수록 효율성이 높다고 판단한다. 이러한 Delay와 관련하여, 아래 Delay1을 종속변수로 설정한다.
즉, Delay1은 Hou and Moskowits(2005)에 의한 가격결정 지연정도를 일별 주가수익률 로써 측정한 값이다.
한편, Hou and Moskowits(2005)의 모형을 본고에서는 개별기업 수익률의 과거값(lag)을 추가하여 새로운 가격지연반응을 측정하고자 한다. 구체적인 수식은 아래와 같다.
위 식은 식 (1)에 개별종목 수익률의 1일전~4일전 실현치를 추가하여 이들 값을 포함 했을 때 delay가 어느 정도로 실현되는지를 검증하기 위한 수식이다. 앞서 정의한 Delay1을 약간 변형한 Delay2를 아래와 같이 설정한다.
셋째, random walk을 측정하는 또 다른 대용치인 Hurst 지수를 사용한다. 이를 모형으로 표현하면 아래와 같다.1)
먼저, u개의 관측치의 시계열 t에 대하여, 평균으로부터의 누적 편차는 다음과 같이 나타낼 수 있다.
이 때 Xt,n은 n 기간동안의 누적편차이고, eu는 u 기간 동안의 일별 주가수익률이며, Mn은 n 기간 동안의 eu의 평균이다.
아래 R은 범위(range)로서, 누적편차의 최대값에서 최소값을 차감한 값이다.
그런데, 범위 R은 시점 또는 시간에 따라 변화하므로, R을 최초의 관측치들의 표준편차 S로 나누어 표준화 되고, Hurst의 경험 법칙에 의해 아래와 같이 R/S 가 추정된다.
이 때 위 식의 양변에 자연로그를 취하면 다음과 같다.
Hurst 지수는 이 같은 log(R/S)와 log(n) 간의 관계를 OLS를 사용하여 추정한다.
즉, log(n)의 회귀계수가 바로 우리가 구하고자 하는 변수인 H 이다(Hurst 지수). 그리고 이러한 Hurst 지수에서 0.5를 차감한 후 절대값을 취하게 되면, 이 값이 작을수록 random walk을 따른다고 볼 수 있다. 이에 본고에서는 random walk에서 멀어진 정도로서 Hurst 지수에서 0.5를 차감한 후 절대값을 취한 값을 Distance_Hurst로 명명하여 주요 종속변수로 설정한다.
넷째, 강건성 분석으로서 먼저 개별종목의 고유위험을 추가적인 종속변수로 설정한다. 기업지배구조가 좋을수록 고유위험이 감소한다면, 이는 우량한 지배구조가 주가의 변동성을 감소시킴으로써 주식시장의 안정성을 높이는 긍정적인 기능을 가지고 있음을 시사하기 때문 이다. 이와 관련하여, 아래와 같이 Idiosyncratic_Risk를 설정한다.
즉, Idiosyncratic_Risk는 고유위험을 1개 사업연도 동안의 일별수익률을 사용하여 산출 하되, 시장모형(market model)을 적용한 후 1-R2으로써 계산한다(Ferreira and Laux, 2007 등). 즉, 종속변수로서 개별기업 수익률을 설정하고, 독립변수로 KOSPI 지수 수익률을 설정한 후(무위험이자율을 차감하지 않으며, 절편이 있는 모형임), 산출된 결정계수 R2을 사용하여 고유위험을 측정하는 것이다.
다섯째, 강건성 검증의 또 다른 분석으로서 일별 주가수익률의 왜도(Skewness)를 종속 변수로 설정한다. 흔히 일별 주가수익률은 양(+)의 왜도를 갖는 것으로 알려져 있는 바, 이는 비정상적으로 큰 수익률이 높은 빈도로 관찰됨을 뜻한다.
따라서 본고에서는 개별기업 1개 사업연도 동안의 일별 주가수익률의 왜도인 Skewness를 설정하여 회귀분석 하기로 한다.
이하 주된 독립변수인 Governance와 나머지 통제변수를 정의하면 아래와 같다.
먼저 Governance는 기업지배구조원에서 제공하는 기업별 지배구조 점수를 사용하되, 각 기업이 취득한 점수를 취득가능 총점으로 나눈 값이다(즉 최대 1점, 최소 0점으로 환산한 값).
이 때 기업지배구조원에서 산출하여 제공하는 기업지배구조 점수의 경우, 크게 4분류의 항목으로부터 도출된다. 첫째. 주주권리 보호 항목이다. 이는 다시 주주권리 보호 및 행사의 편의성, 소유구조, 경영과실의 배분, 그리고 계열회사와의 거래 등 4개의 소분류를 포함하고 있다. 둘째, 이사회이다. 이사회의 경우 이사회의 구성 및 운용, 이사회 평가 및 보수, 이사회 내 위원회 등 3개의 소분류를 포함하고 있다. 셋째, 감사기구이다. 이는 다시 감사기구 구성과 감사기구 운영 등 2항목을 포함하고 있다. 끝으로 공시 항목이다. 이는 다시 공시일반과 홈페이지 정보공개라는 2가지의 세부항목을 포함한다. 이러한 기업지배구조 점수는 평가 대상 기업의 IR 담당자에 의한 설문조사 결과와 함께, 사업보고서의 내용에 기재된 내용을 지수화 하여 계산된다.
다음으로, 정보비대칭 정도를 나타내는 대용변수로서 1/월평균거래량(월평균거래량의 역수)를 사용한다(Bharath et al., 2009). 이 때 거래량의 크기는 곧 informed trading에서 비롯한다는 선행연구(Llorente et al., 2002)가 존재하는 바, 궁극적으로 거래량 및 그 역수는 당연히 정보비대칭의 완화 정도 또는 정보비대칭의 수준을 나타내는 대리변수로서 중요한 의미를 갖는다.
그리고 또 다른 정보비대칭의 대리변수로서 허쉬만-허핀달 지수(Hershman-Herfindahl Index)를 설정한다. 이 같은 HH 지수를 정보비대칭 정도의 대리변수로 사용한 선행연구 로는 Byun et al.(2011)가 있다. 본고에서도 이러한 정보비대칭의 또 다른 대리변수로서 HH 지수를 사용하도록 한다.
한편, 기타 통제변수의 하나로서 EBITDA는 현금흐름을 나타내며, (영업이익+감가상각비)/자산시가총액으로 산출되었다. 이때 자산시가총액은 부채장부가치+자기자본 시가총액으로 계산되었다. 수익성을 나타내는 EBITDA가 클수록 해당 기업은 공시강화 등 좋은 지배구조를 갖출 유인이 증가하고 이에 필요한 자원을 투입할 수 있어 기업경영의 투명성은 높아질 것으로 예상된다. 따라서 모든 종속변수에 대하여 회귀분석 시 회귀계수의 부호는 음(-)의 값을 가질 것으로 예측된다.
Leverage는 부채비율이며, 부채장부가치/자기자본시가총액으로 계산되었다. Size는 시가총액에 자연로그를 취한 값이다. 부채비율이 높을수록 채권자(은행 등)의 감시 기능이 더욱 잘 작동할 것으로 예상된다. 따라서 모든 종속변수에 대하여 회귀분석 시 회귀계수의 부호는 음(-)의 값을 가질 것으로 예측된다.
Residual_Foreign은 외국인 지분율을 종속변수로, 표준화된 지배구조점수를 독립변수로 설정한 후 회귀분석하여 산출한 잔차항(residual)이다. 이는 외국인 지분율이 내생성을 내포하고 있는 바, 표준화된 기업지배구조가 좋을수록 외국인이 더 많은 지분을 매입함으로써 더 높은 지분율을 보유할 수 있기 때문이다. 따라서 본고에서는 외국인 지분율 중 기업지배구조로 설명이 되지 않는 잔차항(Residual_Foreign)을 별도로 산출하여 본고의 주된 회귀 모형에 포함시키도록 한다. 이 때 잔차항에 해당되는 외국인 지분율이 높을수록 경영진 및 지배주주에 대한 감시기능이 더욱 잘 작동할 것으로 예상된다. 따라서 모든 종속변수에 대하여 회귀분석 시 회귀계수의 부호는 음(-)의 값을 가질 것으로 예측된다.
Tobin’s_Q는 자산시가총액을 자산장부가치로 나눈 값이다. 이 변수는 흔히 성장성의 대리변수로도 사용된다. 성장성이 높을수록 이를 뒷받침할 수 있는 자본조달의 중요성이 커지고 이에 따라 투자자들의 신뢰성 확보를 위해 해당 기업의 투명성은 높아질 것으로 예상된다. 따라서 모든 종속변수에 대하여 회귀분석 시 회귀계수의 부호는 음(-)의 값을 가질 것으로 예측된다.
마지막으로, 총자산 증가율(Asset_Growth)을 통제변수에 추가하기로 한다. 총자산 증가율 역시 성장성의 대리변수로서, 이 값이 높을수록 해당 기업의 투명성은 더욱 높을 것으로 예상된다. 따라서 모든 종속변수에 대하여 회귀분석 시 회귀계수의 부호는 음(-)의 값을 가질 것으로 예측된다.
4.3 분석모형 및 가설검증 방법
본 연구의 주요 가설을 검정하기 위한 회귀분석 모형은 기업-연도 고정효과 패널분석 모형이다. 여기에 이분산-자기상관을 통제한 Newey and West(1987)의 표준오차를 사용 한 t-값을 함께 보고하기로 한다.
본고의 고정효과 패널모형을 수식으로 표현하면 아래와 같다
이 때 Governance의 회귀계수가 공히 음(-)의 값을 갖는다면, 본고에서 제시한 모든 가설이 성립하는 것으로 해석한다.
4.4 기초통계량과 상관계수 및 차이분석
본 연구에서 사용되는 변수들에 대한 요약통계량이 <표 1>에 제시되어 있다.
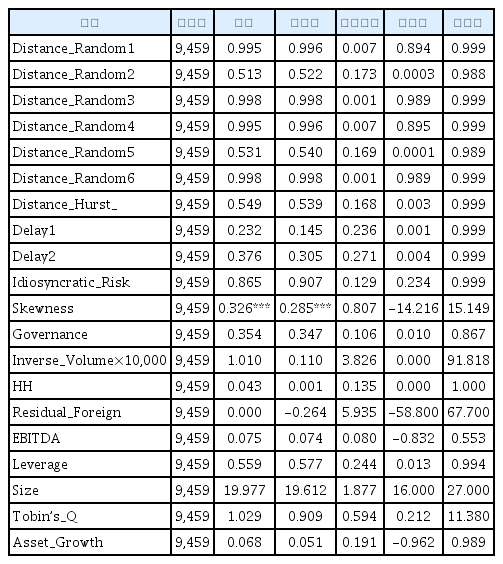
요약통계량
아래 표는 본 연구에서 사용되는 주요 변수들의 요약통계량이다. Distance_Random1은 “1-variance ratio”에 절대값을 취한 값이되, 이 때 variance ratio는 (1개 사업연도간 주별수익률의 분산)/5×(1개 사업연도간 일별수익률의 분산)로 계산되었다(Lo and MacKinlay, 1989). 1-varince ratio의 절대값을 취한 값이 0에 가까울수록, 즉 그 값이 작을수록 주가수익률은 random walk을 따른다고 볼 수 있다. 마찬가지로 Distance_Random2는 “1-variance ratio”에 절대값을 취한 값이되, (1개 사업연도간 월별수익률의 분산)/4×(1개 사업연도간 주별수익률의 분산)로 계산되었다. 역시 마찬가지로, Distance_Random3는 “1-variance ratio”에 절대값을 취한 값이되, (1개 사업연도간 월별수익률의 분산)/20×(1개 사업연도간 일별수익률의 분산)로 계산되었다. Distance_Random4~ Distance_Random6은 GARCH(1,1)을 사용하였을 때 산출된 분산으로써 분산비율을 계산한 후, 앞서 설정한 Distance_Random1~ Distance_Random3을 모방한 값이다. Hurst 지수는 또 다른 random walk을 대리하는 변수이다(자세한 계산법은 본문 참조). Delay1은 Hou and Moskowits(2005)이 제안한 가격결정 비효율성 지표(가격발견의 지연 정도)를 일별 주가수익률로써 측정한 값이며, Delay2는 Hou and Moskowits(2005)의 오리지널 모형에 특정 기업 주가수익률의 과거값을 추가한 후 산출한 delay 지수이다. Idiosyncratic_Risk는 1개 사업연도 동안의 일별수익률을 사용하여 산출하되, 시장모형(market model)을 적용한 후 1-R2으로써 계산되었다(Ferreira and Laux, 2007 등). Skewness는 1개 사업 연도 동안의 일별 주가수익률의 왜도이다. Governance는 기업지배구조원에서 제공하는 기업별 지배구조 점수를 사용하되, 각 기업이 취득한 점수를 취득가능 총점으로 나눈 값이다(즉 최대 1점, 최소 0점으로 환산한 값). Inverse_Volume은 월평균거래량의 역수로서, 표에는 이 값에 10,000을 곱한 값을 나타내었다. HH는 허쉬만-허핀달 지수이다. Residual_Foreign은 외국인지분율을 종속변수로, 표준화된 지배구조점수를 독립변수로 설정한 후 회귀분석하여 얻은 잔차항이다. EBITDA는 현금흐름을 나타내며, (영업이익+감가상각비)/자산시가총액으로 산출되었다. 이때 자산시가총액은 부채장부가치+자기자본 시가총액으로 계산되었다. Leverage는 부채비율이며, 부채장부가치/자기자본시가총액으로 계산되었다. Size는 시가총액에 자연로그를 취한 값이다. Foreign_Share는 외국인 지분율로서, 퍼센트 값으로 표현되었다. Dividend는 1개 사업연도 동안 지급된 현금배당액 총액을 자산시가총액으로 나눈 값이다. Tobin’s_Q는 자산시가총액을 자산장부가치로 나눈 값이다. Asset_Growth는 전년대비 총자산 증가율이다.
먼저 첫 번째 종속변수인 Distance_Random1의 경우, 최소값이 0.894이며 최대값이 0.999로서, 동변수의 표준편차가 매우 작음을 알 수 있다. 이는 KOSPI 시장의 경우 random walk으로부터 상당히 떨어져 있음을 시사한다. 이같은 특징은 Distance_Random3, Distance_Random4Distance_Random6 에서 재확인 된다.
반면 Distance_Random2 및 Distance_Random5의 경우 평균 및 중앙값이 대략 0.5의 값을 가지며, 최소값은 0에 가까운 대신 최대값은 0.99 정로로서, 비교적 큰 표준편차인 0.17의 분포를 확인할 수 있다.
반면, 가격결정 비효율성의 지표인 Delay1과 Delay2의 경우, 평균적으로 0.2~0.4 정도의 값을 갖는 바, 코스피 상장기업의 경우 비교적 주가결정의 비효율성이 다소 낮음을 확인할 수 있다.
다음으로, Idiosyncratic_Risk2의 경우, 평균적으로 80%~90%가 고유위험인 반면 시장험은 10%~20%에 국한됨을 발견할 수 있다.
반면, 일별 주가수익률의 왜도인 Skewness는 대략 0.3 정도로 나타나고 있고 통계적으로 매우 유의한 양(+)의 왜도를 기록하고 있는 바, 이는 코스피 시장이 복권당첨게임(lottery)의 장이 되어왔음을 시사한다.
기타 독립변수 및 통제변수들은 대체로 작지 않은 표준편차를 기록하고 있는 바, 회귀석에 적절한 요건 중 하나를 충족시키고 있음을 확인할 수 있다.
이 외에도 기타 변수간 상관관계는 <표 2>에 나타나 있다. 표에서 가장 중요한, Governance와 종속변수들 간의 회귀계수 대체로 음(-)의 값을 갖는 것으로 나타났다. 이는 Governance가 높을수록 종속변수들은 감소하는, 즉 음(-)의 회귀계수를 갖게 될 것임을 암시한다.
한편, 만일 기업지배구조 수준이 높을 때 본고에서 설정한 종속변수들이 음(-)의 값을 갖는다면, 이는 차이분석을 통해서도 드러날 가능성이 있다. 이에 본고에서는 전체 표본에 대하여 기업지배구조가 양호한 기업들만의 표본과 그리고 취약한 기업들만의 표본, 이렇게 두 표본으로 분리하여 각각의 경우 과연 종속변수를 유의하게 감소시키는지 규명한다. 이같은 차이분석 결과를 <표 3>에 나타냈다. 표에서 알 수 있듯이, 대체로 지배구조가 좋은 기업의 경우 종속변수 값은 더욱 낮았으며, 반대로 지배구조가 취약한 기업의 경우 종속변수의 값은 더욱 높은 경향이 있었다. 이러한 결과는 앞서 상관계수표에서 설명한 것과 유사하게, 본고에서 사용하는 종속변수에 대하여 지배구조수준이 높을수록 더욱 낮은 값을 가질 수 있음을 또한 시사한다.
다만, 통제변수 등이 포함된 회귀분석을 통해서만이 정확한 사실 여부가 확인 가능하다고 하겠다.
5. 실증분석 결과
5.1 기업지배구조가 Variance Ratio에 미치는 영향
앞서 가설 1을 설정하면서, 기업지배구조가 좋을수록 Variance Ratio가 1에 가까울 것이라 추정하였다. 본 절에서는 가설 1이 성립하는지 여부를 고정효과 패널분석을 통해 규명한다. 회귀분석 결과는 <표 4> 및 <표 5>에 나타나 있다.
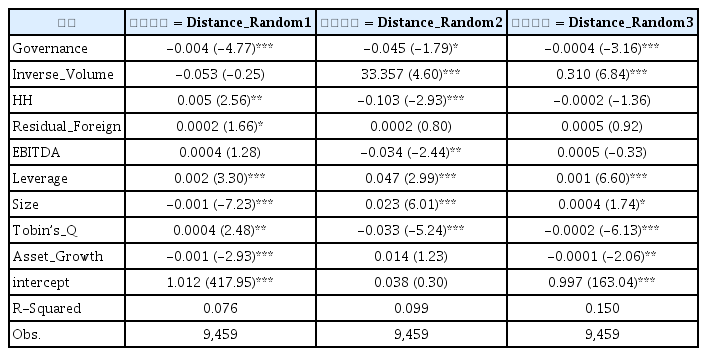
기업지배구조가 Variance Ratio에 미치는 영향
표는 기업지배구조가 좋을수록 Variance Ratio가 1에 가까울 것이지 회귀분석 한 결과이다. 종속 변수는 1에서 variance ratio를 차감한 수치의 절대값이다. 회귀모형은 기업-연도 고정효과 패널분석(firm-year two-way fixed effect panel regression)이다. 표 안의 숫자는 회귀계수이며, 괄호 안의 값은 이분산-자기상관을 통제한 Newey-West의 방법에 의한 t-값이다. ***, **, *은 각각 1%, 5%, 10% 수준에서 통계적으로 유의함을 나타낸다. 변수에 대한 설명은 <표 1> 참조.

기업지배구조가 Variance Ratio에 미치는 영향: GARCH(1,1)을 사용하여
표는 GARCH(1,1)을 사용하여, 기업지배구조가 좋을수록 Variance Ratio가 1에 가까울 것이지 회귀분석 한 결과이다. 종속변수는 1에서 variance ratio를 차감한 수치의 절대값이다. 회귀모형은 기업-연도 고정효과 패널분석(firm-year two-way fixed effect panel regression)이다. 표 안의 숫자는 회귀계수이며, 괄호 안의 값은 이분산-자기상관을 통제한 Newey-West의 방법에 의한 t-값이다. ***, **, *은 각각 1%, 5%, 10% 수준에서 통계적으로 유의함을 나타낸다. 변수에 대한 설명은 <표 1> 참조.
<표 4>에 의하면, 세 가지 방법으로 측정된, 1-variance ratio의 절대값이 기업지배구조가 좋을수록 모두 감소함을 보여주고 있다. 이러한 결과는 기업지배구조가 양호할수록 일별, 주별, 월별 주식가격의 흐름이 공히 보다 더 효율적으로 형성되고 있음을 시사한다.
한편, 본고에서는 GARCH(1,1)을 사용하여 회귀식의 오차항의 분산(MSE)를 추출한 후, 동 분산을 사용하여 앞서 행한 Distance_Random1~Distance_Random3를 모방한 Distance_Random4~Distance_Random6을 설정하였다. 주지하다시피 이들 변수의 공통점은, 이 값이 클수록 random walk 에서 더욱 멀어짐을 의미한다.
이와 같이 Distance_Random4~ Distance_Random6을 종속변수로 설정하여 회귀분석 한 결과, 앞서 제시된 모형들과 같이 모든 경우에 대해서 기업지배구조가 좋을수록, 1-variance ratio의 절대값이 더욱 감소함을 확인할 수 있다. 즉, 주가는 보다 random walk에 가까운 행보를 보였다.
한편, <표 4> 및 <표 5>에 의하면 자산성장률(Asset_Growth)의 회귀계수가 대체로 음(-)의 값을 가져, 성장성이 높을수록 해당 기업의 주가수익률이 대체로 Random Walk을 따르는 것으로 나타났다. 이는 성장성이 높을수록 정보비대칭 정도가 완화됨을 의미한다.
이상을 종합하면, 기업지배구조가 좋을수록 동 종목의 주가수익률은 더욱 random walk을 따름을 알 수 있다. 이는 가설 1이 성립함을 의미한다.
5.2 기업지배구조가 Hurst 지수에 미치는 영향
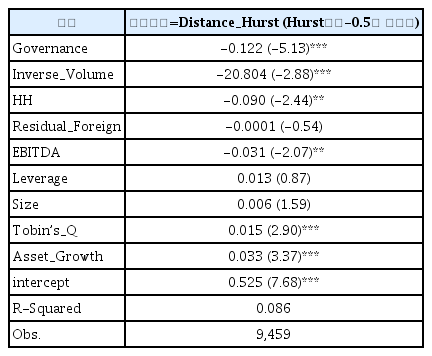
제 5.2절에서는 제 5.1절에서 확인한 결과, 즉 좋은 기업지배구조가 주식가격결정의 효율성을 향상시킨다는 실증결과가, 대용변수(proxy) 또는 측정치를 바꾸어도 즉, Hurst 지수를 사용 하여도 여전히 강건한지 검증한다. 실증분석 결과가 <표 6>에 나타나 있다.
고정효과 패널분석 결과, random walk으로부터 멀어짐을 나타내는 Distance_Hurst를 종속변수로 설정하였을 때, Governance의 회귀계수는 1% 수준에서 유의한 음(-)의 값을 가졌다. 이는 기업지배구조 우수할수록 동 기업의 주가는 더욱 random walk을 따름을 의미한다.
따라서, 가설 2가 성립함을 알 수 있다.
5.3 기업지배구조가 가격결정 지연도에 미치는 영향
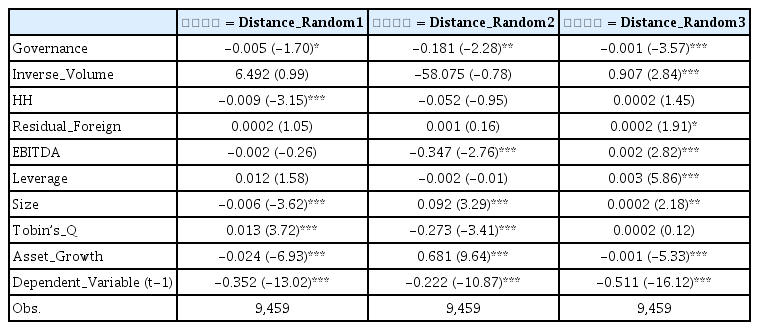
이 절에서는 기업지배구조가 양호할수록 동 기업의 주가가 시장수익률 변화라는 충격이 왔을 때, 지연됨 없이 곧바로 주식가격에 반영 되는지 분석한다. 이를 위하여 먼저 Hou and Moskowits(2005)의 가격결정 지연도를 종속변수로 사용하여 회귀분석 함과 동시에, Hou and Moskowits(2005)의 모형에 과거(lag 값) 개별종목 수익률을 포함한 모형으로써 또 다른 가격결정 지연도를 산출한 후, 동 가격결정 지연도에 Governance가 어떠한 영향을 미치는지 실증분석한다.
실증분석 결과는 <표 7>에 나타나 있다. 실증분석 결과, 서로 다른 두 모형으로부터 산출한 가격결정 지연도(Delay1, Delay2)를 종속변수로 설정하였을 때, Governance는 모두 1% 수준에서 유의한 음(-)의 회귀계수를 가졌다.
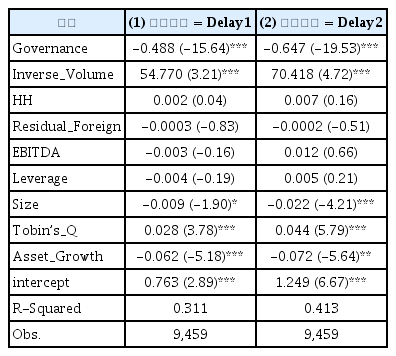
기업지배구조가 주식가격 발견의 지연 정도에 미치는 영향
표는 기업지배구조가 좋을수록 해당 종목의 주식가격 발견의 효율성에 어떠한 영향을 미치는지 회귀분석 한 결과이다. 이 때 주식가격 발견의 효율성 중 하나(식 (1))는 Hou and Moskowits(2005)이 제안한 주식가격 발견의 지연 정도에 의해서 측정되었으며, 다른 하나(식 (2))는 Hou and Moskowits의 모형에 개별종목 주가수익률의 래그값(lag)을 추가한 모형에 의해 측정 되었다. 종속변수(delay1, delay2)는 주식가격 발견의 지연 정도를 각각 나타낸다. 회귀모형은 기업-연도 고정효과 패널 분석(firm-year two-way fixed effect panel regression)이다. 표 안의 숫자는 회귀계수이며, 괄호 안의 값은 이분산-자기상관을 통제한 Newey-West의 방법에 의한 t-값이다. ***, **, *은 각각 1%, 5%, 10% 수준에서 통계적으로 유의함을 나타낸다. 변수에 대한 설명은 <표 1> 참조.
이는 기업지배구조가 우수할수록 가격결정 지연도가 매우 유의하게 감소함을 나타낸다. 즉, 특정 기업의 우수한 지배구조는 동 기업의 주가에 시장정보 뿐만 아니라 과거 자신의 수익률이 더욱 신속하게 반영되는 결과로 해석될 수 있다. 이러한 결과는 주식가격결정의 효율성의 측정치로서 variance ratio를 사용하건, Hurst 지수를 사용하건, Hou and Moskowits(2005)의 측정치를 사용하건 세 종속변수에 대하여 좋은 지배구조가 공히 유 의한 음(-)의 영향을 주고 있음을 강건하게 보여주고 있는 것이다.
한편, <표 7>에 의하면 자산성장률(Asset_Growth)의 회귀계수가 두 회귀모형에 대해 공히 음(-)의 값을 가졌다. 이는 성장성이 높을수록 시장의 정보가 해당 기업의 주가수익률에 지연 반영되는 정도가 더욱 감소함을 의미한다. 이는 성장성이 높을수록 주식가격이 더욱 신속하고 정확하게 결정됨을 의미하는 것으로, 앞서 통제변수 설정시 예측했던 결과이기도 하다.
요컨대, <표 7>을 통해 앞서 설정한 가설 3이 성립함을 알 수 있다.
5.4 강건성 분석
제5.1절~제5.2절에서 발견된 결과, 즉 좋은 기업지배구조가 주식가격결정의 효율성을 증진시키는 긍정적 기능을 가지고 있다는 결과는, 곧 우수한 지배구조가 주식시장에 이와 유사한 또 다른 긍정적인 기능을 가질 것이라는 추정을 가능하게 한다. 이에 본 절에서는 주식가격결정의 효율성 관점 외에 변동성 완화(안정성; 4.3.1) 및 복권당첨 투기성 투자의 완화(4.3.2)에 기업지배구조가 어떠한 역할을 하는지 규명한다.
5.4.1 기업지배구조가 고유위험에 미치는 영향
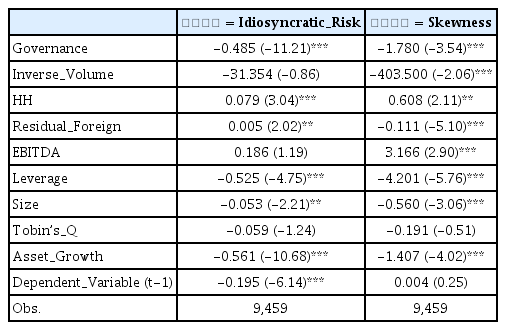
앞서 가설 4를 설정하면서, 기업지배구조가 좋을수록 시장에 보다 양질의 정보가 제공됨으로써 동 종목의 주가의 변동성이 상대적으로 낮을 것이라 추정하였다. 이를 규명하기 위한 실증분석 결과 <표 8>에 정리되어 있다.
<표 8>에 의하면, Idiosyncratic_Risk는, 즉 고유위험은 기업지배구조가 양호할수록 더욱 감소하는 경향이 있음을 확인할 수 있다. 즉, 좋은 지배구조는 주식시장에 noise의 공급을 감소시킴으로써 고유위험을 더욱 낮출 수 있음을 알 수 있다.
한편, <표 8>에 의하면 자산성장률(Asset_Growth)의 회귀계수가 음(-)의 값을 가졌다. 이는 성장성이 높을수록 고유위험은 더욱 감소함을 의미한다. 이는 성장성이 높을수록 주식 가격의 고유변동성이 더욱 낮음을 의미하는 것으로, 앞서 통제변수 설정시 예측했던 결과이기도 하다.
요컨대, 가설 4가 성립함을 확인할 수 있다.
5.4.2 기업지배구조가 주가수익률의 왜도에 미치는 영향
앞서 가설 5를 설정하면서, 기업지배구조가 좋을수록 일별 주가수익률의 왜도(skewness)가 감소할 것이라 추정하였다. 이를 규명하기 위한 실증분석 결과가 <표 9>에 정리되어 있다.
<표 9>에 의하면, 기업지배구조가 양호할수록 일별 주가수익률의 왜도인 Skewness 수준이 더욱 감소하는 경향이 있음을 확인할 수 있다. 즉, 좋은 지배구조는 투자자로 하여금 지나친 복권성향 투자(lottery)를 약화시키는 기능 또한 보유하고 있음을 알 수 있다.
요컨대, 가설 5가 성립함을 확인할 수 있다.
5.5 내생성 통제
제5.5절에서는 기업지배구조의 수준변수(Governance)가 잔차항과 상관관계를 갖는 내생성을 고려하여 논의를 전개하고자 한다.
즉. 기업지배구조가 양호할수록 주식가격결정이 효율적으로 작동할 수도 있지만, 반대로 주식가격결정이 효율적인 기업들이 시장에서의 추가적인 좋은 평판 등을 얻기 위해 지배구조를 우수하게 변화시킬 수 있는 가능성(역의 인과관계)이 있는 것이다. 따라서 이 같은 내생성을 통제하기 위해 본고에서는 패널자료의 내생성을 통제하기 위해 흔히 사용되는 Arelleno and Bond(1991)의 고정효과 동적패널모형을 사용하여 회귀분석 한다. 해당 결과는 <표 10>에 나타나 있다.

내생성의 통제: Arelleno and Bond(1991)의 Dynamic GMM 회귀분석
<표 10-1>~표 10-4>는 기업지배구조 수준 변수(Governance)가 내생성을 가질 수 있는 가능성을 고려하여, 이를 통제하기 위한 Arelleno and Bond(1991)의 Dynamic GMM 회귀분석 결과를 제시하고 있다. 표 안의 값은 회귀계수이며, 괄호 안의 값은 t-값이다. ***, **, *은 각각 1%, 5%, 10% 수준에서 통계적으로 유의함을 나타낸다. 변수에 대한 설명은 <표 1> 참조.
표에서 알 수 있듯이 <표 10-1>부터 <표 10-4>까지의 고정효과 동적패널 회귀분석 결과는, 모든 종속변수에 대하여 기업지배구조 수준(Governance)이 여전히 유의한 음(-)의 값을 갖는 사실을 명시하고 있다. 이는 곧 내생성을 고려하더라도, 본고에서 얻은 실증 결과는 여전히 강건함을 시사하는 것이다.
따라서 본고의 주요 가설, 즉 기업지배구조가 양호할수록 주가가 더욱 random walk를 따르고, 가격지연 현상이 대폭 감소하며, 고유변동성은 하락하고, 왜도는 감소한다는 가설은 내생성을 통제한 후에도 여전히 성립함을 알 수 있다.
5.6 기업지배구조 세부항목 점수가 주식가격결정에 미치는 영향
지금까지 기업지배구조가 주식가격결정에 어떠한 영향을 미치는지, 기업지배구조원이 제공하는 기업지배구조 총점을 기준으로 살펴보았다. 본 절에서는 기업지배구조 총점이라는 관점이 아닌, 지배구조 각론의 점수를 기준으로 각론의 점수가 주식가격결정에 미치는 영향을 고찰한다. 이 때 각론이란, “주주권리보호”, “이사회”, “공시” 및 “감사기구”를 뜻한다.
이 때 각론의 점수는 최저 0점, 최고 1점을 갖는 표준화된 점수(취득점수/만점)를 사용하여 측정한다. 그리고 이 때 기업지배구조 총점이 주식가격결정에 미치는 영향을 살펴볼 때 사용하였던 회귀분석 모형을 동일하게 사용하되, 주요 독립변수만 총점이 아닌 각론의 취득 점수를 설정하여, 각각 성격이 다소 다른 기업지배구조 각론의 취득 점수가 주식가격결정에 어떠한 영향을 미치는지 고찰한다. 회귀분석 결과는 <표 11>(static model) 및 <표 12> (내생성 통제; dynamic model)에 나타나 있다.
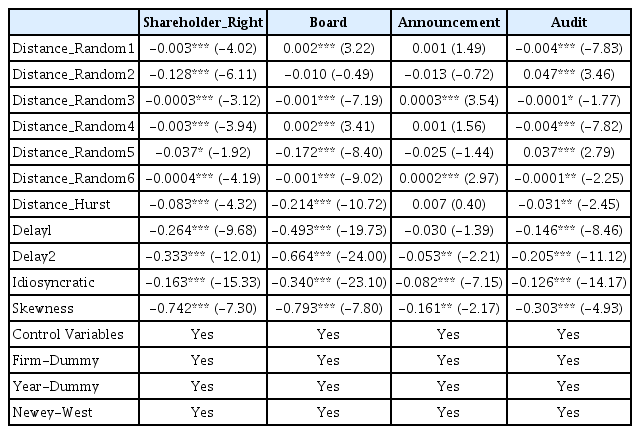
기업지배구조 세부항목이 종속변수에 미치는 영향
표는 기업지배구조 총점을 구성하는 각 항목, 즉 주주권리 보호(Shareholder_Right)와 이사회(Board) 및 공시(Announcement)와 감사기구(Audit)의 수준이 본고의 주요 종속변수에 어떠한 영향을 미치는지 실증분석 한 표이다. 첫 열(column)은 주로 종속변수를 나타내며, 두 번째 열부터 다섯 번째 열까지는 주요 독립변수로서 기업지배구조 세부 항목의 회귀계수 및 t-값을 나타낸다. 회귀모형은 기업-연도 고정효과 패널분석(firm-year two-way fixed effect panel regression)이다. 표 안의 숫자는 회귀계수이며, 괄호 안의 값은 이분산-자기상관을 통제한 Newey-West의 방법에 의한 t-값이다. ***, **, *은 각각 1%, 5%, 10% 수준에서 통계적으로 유의함을 나타낸다. 변수에 대한 설명은 <표 1> 참조.

기업지배구조 세부항목이 종속변수에 미치는 영향: 내생성 통제
표는 기업지배구조 총점을 구성하는 각 항목, 즉 주주권리 보호(Shareholder_Right)와 이사회 (Board) 및 공시(Announcement)와 감사기구(Audit)의 수준이 본고의 주요 종속변수에 어떠한 영향을 미치는지 실증분석 하되, 내생성을 통제하기 위해 Arelleno and Bond(1991)의 방법을 적용한 표이다. 첫 열(column)은 주로 종속변수를 나타내며, 두번째 열부터 다섯번째 열까지는 주요 독립변수로서 기업지배구조 세부 항목의 회귀계수 및 t-값을 나타낸다. 괄호가 없는 수치는 회귀계수를 뜻한다. ***, **, *은 각각 1%, 5%, 10% 수준에서 통계적으로 유의함을 나타낸다. 변수에 대한 설명은 <표 1> 참조.
<표 11>과 <표 12>에서 찾을 수 있는 공통점은, 오직 “주주권리 보호” 항목의 경우만 일관되게 종속변수들에 유의한 음(-)의 영향을 미쳤고, 이사회와 공시 및 감사기구의 경우에는 일부이기는 하나, 유의하지 않은 결과 및 양(+)의 회귀계수를 갖는, 즉 본고의 가설을 지지하지 않는 결과가 나타났다는 사실이다. 결국 기업지배구조 총점이 본 연구의 모든 종속변수에 유의한 음(-)의 영향을 주는 일관된 결과는, 바로 주주권리보호 항목에 의한 것이라 유추할 수 있다. 즉, 주주권리 보호가 더욱 철저하게 지켜지는 기업의 경우에 한하여 지배구조가 좋을수록 주식가격결정이 더욱 효율적으로 형성되며, 그 외 이사회 기능 및 감사기구의 활동과 공정한 공시의 경우에는 일부이기는 하나, 각론의 점수가 높더라도 반드시 주식가격이 효율적으로 결정되지만은 않음을 확인할 수 있는 것이다.
이러한 결과는, 최근 큰 사회적 이슈가 되었고 현재도 중요 이슈로 남아 있는 “기관투자자의 적극적인 의결권 행사”의 시급함과 중요성의 사회적 인지와 무관하지 않다. 즉, 주주권리 보호 장치의 신설 및 기존 제도의 적극적 시행 및 활용은, 결국 이사회 기능의 미비함, 공시의 공정성 상실, 감사기구의 무력화 등을 경험한 우리 사회가, 최적의 해답으로서 기관투자자의 바람직한 의결권 행사를 통한 주주권리보호의 필요성과 시급성을 인지하고 있는 지금의 현실과 일맥상통한 것이다.
요컨대, 기업지배구조 각론 중 오직 “주주권리보호” 측면의 경우만 모든 종속변수에 대하여 유의한 음(-)의 회귀계수 값을 갖는 바, 이는 주식시장에 참여하고 있는 투자자(주주)에게 있어 가장 영향력 있고 실질적인 권리보호 수단이 “주주권리보호”에 초점이 맞춰져 있음을 시사한다. 즉, 이 같은 “주주권리보호”가 잘 되어 있는 기업일수록 주식가격이 더욱 더 효율 적으로 결정됨을 알 수 있다.
6. 결론
본 연구는 KOSPI 기업을 대상으로, 기업지배구조가 좋을수록 과연 주식가격결정의 효율성을 향상시키는지 실증적으로 규명하였다. 본고에서는 주식가격결정의 효율성을 Lo and MacKinlay(1988) 가 제안한 variance ratio 및 Hou and Moskowits(2005)이 제안한 가격결정 비효율성 지표(가격발견의 지연 정도과 Hurst 지수를 그 대용변수로 사용하여 실증분석을 실시하였다.
기업-연도 고정효과 패널분석 및 Newey-West 표준오차를 사용한 실증분석 결과, 기업지배구조가 우수할수록 세 가지 방법으로 측정한 분산비율(variance ratio)의 값이 더욱 1에 근접하였다. 이러한 결과는 GARCH(1,1)에 의한 분산(MSE)을 사용하여 분산비율을 산출하여도 종속변수에 미치는 영향이 여전히 강건하였다.
또한 Hurst 지수의 함수를 종속변수로 사용하여도, 즉 동 지수에서 0.5를 차감한 후 절대값을 취한 수치를 (Distance_Hurst) 사용하여도, 지배구조가 양호할수록 Distance_Hurst가 감소함으로써 동 주식은 더욱 더 random walk를 따르는 것으로 나타났다.
그리고 기업지배구조가 양호할수록 가격결정의 지연정도는 감소한 바, 동 가격결정의 지연 정도로서 Hou and Moskowits(2005)의 방법에 의한 지연도를 사용하여도, 그리고 동 모형에 개별 종목 수익률의 과거값(lag-값)을 포함한 모형을 의한 지연도를 사용하여도, 실증결과는 강건하였다.
한편, 강건성 분석을 위해 고유위험(idiosyncratic volatility), 왜도(skewness)를 종속변수로 사용한 패널분석 결과, 기업지배구조가 양호할수록 고유위험이 감소하여 주가의 안정성이 증가되었고, 왜도가 감소하여 복권당첨 성향의 투자성향이 감소한 것으로 나타났다.
나아가 본 연구의 핵심변수인 Governance(지배구조수준)가 잔차항과 상관관계를 갖는 내생성을 통제하여도, 즉 역의 인과관계의 가능성을 통제하여도, 여전히 Governance는 가격결정의 비효율성에 음(-)의 영향력을 행사하는 것으로 분석되었다.
그리고 이러한 기업지배구조가 주식가격결정에 긍정적 영향을 미친다는 사실은, 이사회와 공시 및 감사기구 등 여타의 세부항목 보다는 “주주권리보호”에 의해 유도된 바가 크다고 할 수 있었다. 즉, 주식시장에 참여하고 있는 투자자(주주)들이 가장 실효성 있고 의미 있다고 판단하고 있는 지배구조 세부항목은 바로 주주권리보호라는 사실을 확인할 수 있었다.
이러한 결과는 좋은 기업지배구조, 특히 주주권리보호가 주식가격 결정의 효율성을 더욱 향상시키는 것을 의미하는 바, 이는 기존의 좋은 기업지배구조의 필요성을 주장하는 일련의 연구들과 맥을 같이 한다.
한편, Gompers et al.(2003)에 의하면 주주권리보호가 가장 잘 이루어지는 종목을 매입하고 주주권리보호가 가장 많이 위배되는 종목을 매도하였을 경우, 벤치마크 대비 초과수익률이 연평균 8.5%에 달함을 보고한 바 있다. 이러한 현상은 일종의 이상현상(anomaly)으로 볼 수도 있는데, 그 이유는 어떤 기업의 지배구조의 수준이 양호할수록 동 기업은 더욱 높은 수익률을 상당기간 동안 향유하는 패턴을 갖는 것과 동시에 지배구조 수준이 취약할수록 동 기업은 더욱 낮은 수익률을 갖는 패턴을 갖고 있기 때문이다. 이들은 일종의 차익거래 이익을 수익률로 나타낸 것인 바, 이러한 차익거래 이익은 주식시장이 균형상태로 되돌아가면서 자연스럽게 사라지기 마련이다. 그런데 중요한 사실은 지배구조 수준에 따른 투자라는, 매우 단순한 패턴으로 인한 차익거래 이익이 사라지지 않는다는 것에 있다. 특히 기업지배구조가 나쁜 것이 일종의 경영상의 잠재적 위험을 반영하는 것이라면 이러한 기업의 주가수익률은 오히려 기업지배구조가 좋은 기업의 주가수익률을 상회하여야 할 것이다. 이런 점에서 앞에서 언급한 Gompers et al.(2003)의 결과는 이상현상으로 해석되어 왔다.
반면에 본 논문의 연구결과에 따르면 이처럼 차익거래 이익을 제공하는 패턴이 사라지지 않는 이유는 의외로 단순한 논리로써 설명 가능하다. 즉, 지배구조가 우량한 기업의 경우, 해당 기업과 관련된 정보가 주식시장에 도착했을 때 그 즉시 동 종목의 주식가격에 반영 되는 수준이 상대적으로 높은 반면, 지배구조가 취약한 기업의 경우 주식시장에 양질의 정보가 도착했음에도 불구하고 주식가격에 반영되는 속도가 상대적으로 느리면서 또한 부 정확할 것이다. 따라서, 예를 들어, 주식가격 결정에 있어 높은 효율성을 보이는 종목에 대한 수요는 점차 증가할 것인 반면, 주식가격 결정에 있어 낮은 효율성을 보이는 종목에 대한 수요는 점차 감소할 것이다. 전자의 경우 주식가격의 상대적 상승이 점차적으로 이루어질 것이며, 후자의 경우는 주식가격 하락(또는 낮은 상승)이 점차적으로 관찰될 것이다. 따라서 앞서 언급한 차익거래 이익이 사라지지 않는 것은 이상현상이라기 보다는 지배구조에 따른 투자자의 선호(preference)를 반영한 합리적 선택의 결과라 볼 수 있다.
요컨대, 기업지배구조 수준은 주식가격 결정의 효율성을 좌우할 수 있으며, 이상현상으로 간주되는 지배구조 수준에 따른 투자로 인한 차익거래 이익 또한 합리적으로 설명 가능함을 알 수 있다.
Notes
Chang and Kim(1999) 부분 인용.