소비관련 거시변수를 사용한 조건부 자산가격모형의 설명력에 관한 연구^*

Evaluating the Conditional CAPM using Consumption-based State Variables: Evidence from the Korean Stock Market^*

Article information

Korean J Financ Stud. 2021;50(3):339-367

Publication date (electronic) : 2021 June 30

doi : https://doi.org/10.26845/KJFS.2021.06.50.3.339

Dojoon Park ^,, Young Ho Eom , Jaehoon Hahn

박도준^,, 엄영호, 한재훈

(연세대학교 연구교수)

Research Professor, Yonsei University

(연세대학교 교수)

Professor, Yonsei University

(연세대학교 교수)

Professor, Yonsei University

^** Corresponding Author. Address: Yonsei Business School, Yonsei University, 50 Yonsei-ro, Seodaemun-gu, Seoul, Korea, 03722; E-mail: dojoon@yonsei.ac.kr; Tel: +82-2-2123-6861; Fax: +82-2-2123-8639.

^** 연락담당 저자. 주소: 서울특별시 서대문구 연세로 50 연세대학교 경영대학, 03722; E-mail: dojoon@yonsei.ac.kr; Tel: 02-2123-6861; Fax: 02-2123-8639.

*This work was supported by the ‘BK21 FOUR (Fostering Outstanding Universities for Research)’ in 2021 and is based on Chapter 6 of Dojoon Park’s PhD dissertation at Yonsei University.*이 논문은 2021년도 ‘4단계 두뇌한국21 사업(4단계BK21 사업)’에 의하여 지원되었으며, 박도준의 연세대학교 박사학위논문 중 6장을 수정 및 보완하여 작성된 것임을 밝힙니다.

Received 2020 July 27; Revised 2021 February 15; Accepted 2021 March 5.

Abstract

본 연구에서는 소비관련 거시변수를 상태변수로 사용한 조건부 자산가격모형의 설명력을 실증적으로 분석하였다. 분석의 기본모형은 CAPM, 인적자본 모형, 소비 CAPM 및 3요인 모형이다. 분석에 사용된 상태변수는 세 가지 소비관련 거시변수로, Lettau and Ludvigson(2001)의 총자산 대비 소비비율, Campbell and Cochrane(1999)의 잉여소비비율 및 Santos and Veronesi(2006)의 소비 대비 소득비율이다. 분석에는 기업규모, 장부가치 대 시장가치, 거래회전율, 고유위험 및 산업 등으로 분류된 주식 포트폴리오를 사용하였다. 실증분석 결과, 소비관련 변수를 상태변수를 사용한 조건부모형의 설명력은 비조건부모형에 비해 개선되었으며, 특히 소득증가율을 포함하는 조건부 인적자본 모형의 설명력은 Fama and French(1993)의 3요인 모형과 유사한 수준의 설명력을 가지고 있는 것으로 나타났다. 본 연구는 이론과 밀접한 관련을 가지는 거시경제변수에 기초한 모형으로 한국 주식시장의 횡단면적 수익률 차이를 설명할 수 있음을 보였다는 점에서 의미가 있다.

Trans Abstract

In this study, we evaluate the empirical performance of conditional asset pricing models using consumption-based measures as state variables. We incorporate three consumption variables known to forecast the equity risk premium as conditioning variables to capture time variations in the risk premium. These three variables are the consumption-aggregate wealth ratio, the surplus consumption ratio, and the labor income to consumption ratio. The asset pricing models evaluated in this study are the CAPM, the CAPM with human capital, the consumption CAPM, and the Fama-French three-factor model. We compare the unconditional and conditional specifications of these four asset pricing models using the two-pass cross-sectional regression methodology, using the size, book-to-market, turnover, and idiosyncratic risk sorted portfolios and sector portfolios as test assets. We demonstrate that the conditional CAPM with human capital performs far better than the unconditional specifications and about as well as the Fama and French three-factor model in explaining the cross-section of average stock returns in Korea.

Keywords: Conditional CAPM; Consumption; Consumption-Aggregate Wealth Ratio; Surplus Consumption Ratio; Income To Consumption Ratio

Keywords:

Keywords: 조건부 CAPM; 소비; 총자산 대비 소비비율; 잉여소비비율; 소비 대비 소득비율

1. 서론

자본자산가격결정모형(Capital Asset Pricing Model; 이하 CAPM)은 시장균형상태에서 위험자산 또는 포트폴리오의 수익률을 시장 포트폴리오의 수익률과 체계적 위험을 나타내는 베타로 설명한다(Sharpe, 1964; Lintner, 1965; Mossin, 1966). 하지만 1980년대 이후 주식 포트폴리오의 횡단면적 수익률 차이를 CAPM의 베타로 설명할 수 없는 다양한 이상현상들(anomalies)이 실증분석에서 발견되었으며, 이와 같은 이상현상을 설명하기 위해 CAPM의 대안으로 다요인 모형(multi-factor model)이 제안되었다. Fama and French (1993)가 제시한 3요인 모형 등의 다요인 모형은 CAPM 대비 우월한 설명력을 보여주는 반면 모형의 체계적 위험요인(risk factor)이 이론적 근거가 취약한 포트폴리오 수익률이라는 근본적 한계를 가지기 때문에 위험요인의 경제적 의미에 대한 해석이 어렵다. 반면 소비 혹은 노동소득 등의 거시변수를 위험요인으로 도입한 자산가격모형, 또는 거시변수를 자산가격모형의 상태변수(state variable)로 추가한 조건부 자산가격모형 등은 위험자산의 수익률 차이를 거시변수의 변동과 연관시킬 수 있다는 점에서 상대적으로 견고한 이론적 근거를 가진다고 할 수 있다.

본 연구의 목적은 소비관련 거시변수를 시간가변적 위험프리미엄을 반영하는 상태변수로 포함하는 조건부 자산가격모형의 설명력을 실증적으로 분석하는 것이며, 분석의 기본 모형으로는 CAPM, 소득증가율을 위험요인으로 포함하는 인적자본 모형, 소비증가율이 위험요인인 소비 CAPM 및 Fama and French(1993)의 3요인 모형을 사용하였다. 국내의 주식시장 분석에 거시변수를 사용한 자산가격모형을 적용한 선행연구는 많이 있으나 조건부 자산가격모형, 특히 소비관련 거시변수를 상태변수로 사용한 연구는 드문 편이다.¹^,) 본 연구는 Lettau and Ludvigson(2001), Campbell and Cochrane(1999), Santos and Veronesi (2006) 등이 제시하고 이후 실증분석에 널리 적용되고 있는 총자산 대비 소비비율, 잉여소비비율 그리고 소비 대비 소득비율 등의 세 가지 소비관련 거시변수를 조건부 자산가격모형의 상태변수로 포함한 경우 국내 주식시장 수익률의 횡단면적 차이와 유의적인 연관을 가지는 지를 총체적으로 분석하였다는데 의의가 있다.

조건부 자산가격모형에서 상태변수로 사용되기 위한 기본적 조건 중 하나는 시장의 초과수익률 또는 위험프리미엄에 대한 예측력이라고 할 수 있다. Park et al.(2019)은 Lettau and Ludvigson(2001), Campbell and Cochrane(1999), Santos and Veronesi(2006)의 등이 제시한 총자산 대비 소비비율, 잉여소비비율 그리고 소비 대비 소득비율을 한국 자료의 특성과 한계를 반영하여 구성한 후, 이 거시변수들의 위험자산 초과수익률에 대한 예측력을 검증하였다. 이에 본 연구는 Park et al.(2019)의 연구에서 국내의 주식 초과수익률에 대한 예측력이 검증된 세 가지 소비관련 거시변수를 상태변수로 사용하였다.

분석에 사용된 소비관련 거시변수 중 Lettau and Ludvigson(2001)의 총자산 대비 소비비율은 대표 경제주체의 예산제약식으로부터 도출되었다. 도출된 식에 따르면, 위험프리미엄은 시간가변적이며 총자산 대비 소비비율과 미래의 자산수익률 또는 위험프리미엄은 양(+)의 상관관계를 가지고 있다. Campbell and Cochrane(1999)은 전체 소비자의 총 소비수준을 습관으로 정의하고 이를 초과하는 소비인 잉여소비에 따라 소비자의 효용이 결정되는 모형을 제시하였고 잉여소비를 소비로 나눈 잉여소비비율은 경기역행적이며, 투자자의 위험회피도를 반영한다고 주장하였다. 한편 Santos and Veronesi(2006)는 소비의 재원이 근로소득과 금융자산의 배당으로 구성된다면, 전체 소비 중 근로소득으로 재원이 조달되는 비중이 위험프리미엄의 변화에 대한 정보를 가진다고 주장하였다.

본 연구에서는 소비관련 거시변수를 상태변수로 포함하는 조건부 모형의 바탕이 되는 기본 모형으로 CAPM, Jagannathan and Wang(1996) 인적자본 모형, 소비증가율을 위험요인으로 설정한 단순한 소비 CAPM 및 Fama and French(1993)의 3요인 모형을 고려하였다. Jagannathan and Wang(1996)은 시장포트폴리오에 포함되는 위험자산에 인적자본을 포함시켜야 한다고 주장하고, 인적자본 수익률의 대용으로 노동소득증가율을 포함하는 인적자본 모형을 제시하였다. 소비 CAPM에 따르면, 합리적 투자자는 주어진 투자기회에서 소비를 평활화(consumption smoothing)하는 방법으로 효용을 극대화하고, 소비에 대한 한계효용은 소비가 증가할 수록 감소한다. 따라서 투자자는 소비에 대한 민감도가 높은 자산에 대해 위험프리미엄을 요구한다. 3요인 모형은 CAPM의 위험요인에, 기업규모(size) 위험과 장부가치 대 시장가치(book to market) 위험의 모방 포트폴리오를 추가한 모형이다.

실증분석의 대상 포트폴리오는 기업규모 및 장부가치 대 시장가치 비율의 두 가지 기준으로 분류한 16개 포트폴리오를 사용하였다. Lewellen et al.(2010)은 자산가격모형의 횡단면 실증분석은 분석의 대상 포트폴리오에 따라 모형의 설명력이 높게 측정될 수도 있으므로, 실증분석에 분석대상 포트폴리오를 추가하는 해법을 제안하였다. 이러한 시사점을 고려하여, 기업규모 및 장부가치 대 시장가치 비율의 두 가지 기준으로 분류한 16개 포트폴리오에 주식 거래회전율 및 기업 고유위험으로 분류된 5분위 포트폴리오 10개와 KOSPI의 산업별 포트폴리오 18개를 추가하여 총 44개 포트폴리오를 대상으로 강건성 검증을 실시하였다. 실증분석 결과 상태변수를 사용한 조건부 모형의 설명력이 비조건부 모형에 비해 설명력이 많이 향상된 것으로 해석이 가능하며, 상태변수를 사용한 조건부 인적자본 모형의 설명력이 3요인 모형과 유사한 수준의 설명력을 가지고 있는 것으로 나타났다. 또한 3요인 모형에 상태변수를 사용하는 경우에도 그 설명력이 향상되는 결과를 얻을 수 있었다. 이는 소비관련 거시변수가 3요인 모형이 설명하지 못하는 주식 수익률의 횡단면적 차이에 대한 설명력을 가지고 있다고 유추해 볼 수 있다.

Fama and French(1993)의 3요인 모형과 같이 체계적 위험요인의 대용치로 모방 포트폴리오를 사용한 다요인 자산가격모형은 포트폴리오의 수익률 차이에 대한 횡단면적 설명력이 상대적으로 높다는 장점이 있다.²) 하지만 CAPM이 설명하지 못하는 포트폴리오 특성을 이용하여 모방 포트폴리오를 만들었기 때문에 모형의 설명력이 당연히 향상될 수 있다는 점과 기업특성에 바탕을 둔 모방 포트폴리오와 체계적 위험요인의 연관성에 대한 이론적 근거가 부족하다는 점에서 그 한계가 있다. 반면에 거시변수를 위험요인으로 포함하는 자산가격모형 또는 소비관련 거시변수를 상태변수로 사용한 조건부 자산가격모형은 주식 포토폴리오 간 횡단면적 수익률 차이를 거시경제변수의 변화 및 이론에 기반한 모형으로 설명하였다는데 그 의의가 있다.

본 논문의 구성은 다음과 같다. 제 2장은 분석의 기본모형인 CAPM, 인적자본 모형, 소비 CAPM, 3요인 모형 및 분석 방법을 설명하였으며, 분석에 사용된 소비관련 거시변수, 자료 및 포트폴리오 구성방법에 대해 기술하였다. 제 3장은 추정결과와 강건성 검증결과를 정리하였다. 제 4장은 결론을 제시한다.

2. 분석모형과 방법 및 자료

2.1 분석모형 및 방법

분석의 기본모형 또는 비조건부모형은 CAPM, 인적자본 모형, 소비 CAPM 및 3요인 모형이다. CAPM의 위험요인은 시장위험 한가지이며, 시장위험으로 모든 개별 위험자산의 수익률을 설명한다. 주가지수가 시장위험 또는 시장포트폴리오의 대용치라면, 주가지수의 초과수익률(이하 MKT)이 시장위험이 된다.

시장위험은 모든 위험자산을 포괄하지만, 그 대용치(proxy)로 주가지수를 사용하는 경우 주식 이외의 위험자산이 제외되는 문제가 있다. Jagannathan and Wang(1996)은 소비자의 전체 자산 중 인적자본의 비중이 상대적으로 크기 때문에 이를 위험자산 범위에 포함시켜야 한다고 주장하였다. 소득은 인적자본에서 발생하는 현금흐름이므로, 인적자본 모형은 소득증가율(Δy)을 인적자본 수익률의 대용치로 사용한다. 인적 자본모형의 위험요인은 MKT와 소득증가율 두 가지이다.

대표 경제주체의 소비 효용함수가 시간분리의 효용함수(time separable power utility)인 경우, 추계적 할인요인은 소비증가율의 선형함수로 근사될 수 있다(Ludvigson, 2013). 소비 CAPM의 체계적위험은 소비증가율(Δc)이다. 합리적 투자자는 주어진 투자기회에서 소비를 평활화(consumption smoothing)하는 방법으로 효용을 극대화하고, 소비에 대한 한계효용은 소비가 증가할 수록 감소한다. 따라서 투자자는 소비에 대한 민감도가 높은 자산에 대해 높은 위험프리미엄을 요구한다.

다요인 모형인 Fama and French(1993)의 3요인 모형은 CAPM의 위험요인에, 기업규모(size) 위험과 장부가치 대 시장가치(book to market) 위험의 모방 포트폴리오를 추가한 모형이다. 기업규모 위험의 모방 포트폴리오(이하 SMB)는 소규모 기업을 매입하고 대규모 기업을 매도하는 포트폴리오이고, 장부가치 대 시장가치의 위험 모방 포트폴리오는(이하 HML)은 장부가치 대 시장가치 비율이 높은 기업을 매입하고 비율이 낮은 기업을 매도하는 포트폴리오이다. 기존 연구에서 소형주의 평균수익률이 대형주에 비해 높고, 장부가치 대 시장가치의 비율이 높은 가치주의 평균수익률이 비율이 낮은 성장주에 비해 높기 때문에, SMB와 HML의 평균수익률은 양(+)의 값을 가질 것으로 예상된다.

k개의 위험요인(f)을 가지는 비조건부모형은 식 (1)와 같이 선형의 추계적 할인요인(stochastic discount factor 또는 pricing kernel) 모형으로 표시할 수 있다.a는 상수이며 b’는 k개의 상수 벡터이다.

(1)m=a+b′ f

추계적 할인요인(m)의 계수는 시간에 따라 변화할 수 있으므로, 조건부 자산가격모형은a와b’가 상태변수에 영향을 받아 변화할 수 있다고 가정한다. 한 개의 위험요인(f_t)을 가지는 조건부 자산가격모형의 추계적 할인요인(m_t)은 식 (2)와 같이 표현할 수 있다. 모형의 계수a_t-1와 b_t-1는 시간가변적이다.

(2)mt=at−1+bt−1ft

조건부 자산가격모형의 계수 a_t-1 와 b_t-1를 식 (3)과 같이 상태변수(SV_t-1)의 선형함수라고 가정하면, 식 (3)의 마지막 식과 같이 세 가지의 위험요인(SV_t-1, f_t, SV_t-1^.f_t)을 갖는 모형으로 표시할 수 있다. 식 (3)에서 a₀, a₁, b₀ 및 b₁ 은 상수이다. 즉 하나의 위험요인과 하나의 상태변수를 갖는 조건부모형은 세 가지의 위험요인을 가지는 비조건부모형과 같다.

(3)mt=a(SVt−1)+b(SVt−1)ft =a0+a1SVt−1+(b0+b1SVt−1)ft =a0+a1SVt−1+b0ft+b1SVt−1·ft

각각 한 개의 위험요인과 상태변수를 가지는 조건부 CAPM과 조건부 소비 CAPM은 각각 3개의 위험요인을 갖는 비조건부모형이 되고, 두 개의 위험요인과 한 개의 상태변수를 가지는 조건부 인적자본 모형은 5개의 위험요인을 갖는 비조건부모형이 된다. 3요인 모형의 경우는 위험요인 중 MKT의 계수만을 소비관련 거시변수의 선형함수로 가정하였기 때문에, 위험요인이 5개인 비조건부모형과 같아진다.

선형의 추계적 할인요인 모형은 식 (4)와 같이 위험자산(i)의 초과수익률(Rie)을 각각 k개의 위험지표인 베타(β_i)와 그 위험프리미엄(λ)으로 표현할 수 있다. 따라서 분석에 사용되는 모든 비조건부모형 및 조건부모형은 식 (4)와 같이 표현할 수 있다.

(4)E(Rie)=γ+λβi

식 (4)의 위험프리미엄(λ) 추정은 Fama and MacBeth(1973)의 시계열 회귀분석 및 횡단면 회귀분석의 2단계 추정방법을 사용한다. 식 (5)는 2단계 추정방법 중 첫 번째 단계인 시계열 회귀분석의 식이다. 종속변수인 개별 포트폴리오(i)의 분기 초과수익률(Ri,te)에 대해서, 설명변수인 k개의 위험요인(f_t)에 대한 민감도(β’_i)를 추정한다.

(5)Ri,te=αi+β′ift+εi,t

시계열 회귀분석의 민감도(β’_i) 추정치를 사용하여 식 (6)의 횡단면 회귀분석으로 위험프리미엄(λ)을 추정한다. 위험프리미엄(λ) 추정치의 유의성 검증에는 2단계 회귀분석에 따른 오류를 조정한 Shanken(1992)의 표준오차를 사용하고, 횡단면 분석의 조정된 결정계수(R²)의 계산은 종속변수로 포트폴리오의 평균 초과수익률을 사용하여 계산하는 Jagannathan and Wang(1996)의 방법을 사용한다. 결정계수의 극단값에 따른 영향을 보안하기 위해 식 (6)의 횡단면 회귀분석 잔차(υ_i)의 평균절대오차(Mean Absolute Error; 이하 MAE)를 계산하고, 평균제곱근오차(Root Mean Square Error; 이하 RMSE)를 함께 보고한다.

(6)E(Ri,te)=γ+λβi+υi

CAPM과 Fama and French(1993)의 3요인 모형의 위험요인은 포트폴리오의 초과수익률이며, 그 기댓값이 위험프리미엄(λ)이다. 분석에 개별 포트폴리오의 초과수익률을 사용하는 경우 모형의 설명력이 높다면 시계열 회귀분석 식 (5)의 상수항(α_i)은 0이 되어야 하고, 각 포트폴리오 별로 추정된 상수항이 0인지 여부를 검정할 수 있다. 반면 인적자본 모형, 소비 CAPM 및 거시변수를 상태변수로 사용한 조건부모형의 위험요인은 포트폴리오의 수익률이 아니기 때문에 상수항이 0인지에 대한 검증을 위해서는 위험요인의 값을 조정해야 한다. 식 (5)에 기대값을 취하고, 식 (4)에서 γ 가 0이라면 상수항(α)은 식 (7)과 같다. 이를 다시 식 (5)에 대입하면 식 (8)과 같아진다.

(7)αi=βi′(λ−E(ft))

(8)Ri,te=βi′(ft−E(ft)+λ)+εi,t

식 (8)에 의하면, 시계열 회귀분석의 상수항이 0이 되기 위해서는 거시변수인 위험요인(f_t)의 값을 조정해야 한다. 우선 시계열 회귀분석의 추정된 민감도(β’_i)를 이용하여, γ가 0인 경우의 위험프리미엄(λ)을 추정한다. 위험요인을 평균이 0이 되도록 조정(f_t-E(f_t))하고, 다시 위험프리미엄의 추정치(λ) 만큼 더해준다. 조정된 위험요인으로 다시 시계열 회귀분석을 실시하면 상수항(α_i)의 추정치는 식 (8)에 따라 0이 되어야 한다.

시계열 회귀분석의 상수항에 대한 Gibbons et al.(1989)의 F-검정(이하 GLS F-검증)은 시계열 회귀분석에서 ‘개별 포트폴리오의 상수항이 모두 0이다.’라는 귀무가설에 대한 검정이다. Fama and French(1993)는 모형의 설명력이 높아서 시계열 분석의 잔차(ε_i,t)가 작고 추정된 상수항이 대체로 0에 근접하는 경우, 상대적으로 상수항의 추정치가 큰 포트폴리오의 영향으로 GRS F-검증이 기각될 수 있다고 설명하였다. Fama and French(1996)는 3요인 모형으로 추정된 개별포트폴리오의 위험요인에 대한 민감도 패턴이 포트폴리오의 수익률 패턴과 일치함을 보이며, GRS F-검증이 기각되더라도 모형의 설명력이 높을 수 있다고 설명하였다. 시계열분석의 상수항에 대해 GRS F-검증에 추가하여 포트폴리오별 상수항의 절대값에 대한 평균값(Mean Absolute Pricing Error; 이하 MAPE)과 포트폴리오별 상수항 제곱의 평균을 다시 제곱근한 값(Root Mean Square Pricing Error; 이하 RMSPE )을 계산하여 모형간 설명력을 비교한다.

2.2 소비관련 거시변수

조건부 자산가격모형의 실증분석을 위해서는 위험자산의 초과수익률 또는 위험프리미엄에 대한 예측력을 가지고 있는 상태변수가 필요하다. 본 연구에서는 상태변수로 Park et al.(2019)의 연구에 사용된 총자산 대비 소비비율, 잉여소비비율 그리고 소득 대비 소비비율 등 세 가지 소비관련 거시변수를 사용한다. Lettau and Ludvigson(2001), Campbell and Cochrane(1999), Santos and Veronesi(2006) 등이 제시한 세 가지 소비관련 거시변수는 이론적 근거와 더불어 실증분석에서 유의한 설명력을 보여주었다. Park et al.(2019)은 세 가지 변수를 국내 거시통계자료의 특성을 반영하여 우리나라의 소비관련 거시변수를 계산하였는데, 실증분석에서 주식, 채권 및 부동산의 장기 초과수익률에 대한 예측력이 보고되었다.

시간가변적 위험프리미엄에 대한 정보를 반영하는 총자산 대비 소비비율인 cay는 로그 1인당 소비(c_t), 로그 1인당 자산(a_t) 그리고 로그 1인당 소득(y_t)의 공적분 관계식의 잔차이다. Lettau and Ludvigson(2001a)은 대표 경제주체의 예산제약식으로부터 소비, 물적자산, 인적자산 및 미래 자산수익률(r_a,t+i) 간의 관계를 나타내는 식 (9)를 도출하였다.

(9)ct−ωat−(1−ω)yt=Et∑i=1∞ρwi(ωra,t+i+(1−ω)Δyt+i−Δct+i)

식 (9) 오른쪽의 세 변수 자산수익률(r_a,t+i), 소득증가율(Δy_t+i), 소비증가율(Δc_t+i)이 정상성(stationary)을 갖는다면 c_t, a_t, y_t는 공적분 관계에 있으며, 공적분의 잔차(c_t - ωa_t-(1-ω)y_t)인 cay는 미래의 자산수익률(r_{a, t+i}) 또는 시간가변적인 리스크프리미엄(time-varying risk premium)에 대한 정보를 가질 수 있다. 식 (9)에 따르면 총자산 대비 소비비율과 미래의 자산수익률 또는 위험프리미엄은 양(+)의 상관관계를 가지고 있다. Lettau and Ludvigson(2001a, 2001b)은 미국의 소비, 자산 및 소득자료로 추정한 총자산 대비 소비비율이 미래의 주식 초과수익률에 대한 예측력이 있음을 보였으며, 총자산 대비 소비비율을 상태변수로 사용하여 조건부 자산가격모형의 설명력을 실증분석하였다.

Park et al.(2019)은 외국 연구사례의 통계자료와 우리나라의 통계자료를 비교하고, 주어진 자료의 제약하에서 국내 자료의 특수성을 고려하여 소비관련 거시변수를 구성하였다. 우리나라의 소비는 가계의 비내구재와 서비스에 대한 최종소비지출로 계산하였다. 우리나라의 자산통계는 토지 등의 부동산에 대한 통계의 존재 여부와 통계기준 또는 집계방식의 변경에 따른 자료의 비연속성 문제가 있다. 자산은 비금융생산자산과 금융자산의 합으로 계산하였는데, 비금융생산자산의 포함여부에 따라 두 가지 변수로 정의하였고, 소득의 경우 자영업자의 근로소득 포함여부에 따라 역시 두 가지 변수로 정의 하였다. 자산과 소득의 계산 방법에 따라 총 4가지의 총자산 대비 소비비율을 계산하였는데, 이중 금융자산 만을 자산에 포함하고 자영업자의 근로소득을 포함한 소득으로 계산한 총자산 대비 소비비율이 위험프리미엄에 대한 예측력이 통계적으로 가장 유의하게 나타났다.

Campbell and Cochrane(1999)의 잉여소비비율(SURP)은 전체소비 중 습관(Hte)을 초과하는 소비(C_t)인 잉여소비(Ct−Hte)의 비율이다. 경기 호황기에 소비가 증가하면 잉여소비비율은 1에 근접하고 불황기에 소비가 습관(Hte) 수준으로 감소하면 0에 수렴한다. 따라서 잉여소비비율은 경기변동과 양(+)의 관계를 갖는다. 소비자의 효용이 잉여소비에 의해 결정된다면, 효용함수의 기울기 또는 위험회피도는 잉여소비비율과 역의 관계를 가지게 된다. 즉 소비가 증가하는 호황기에는 상대적으로 투자자가 요구하는 위험프리미엄이 낮고, 불황기에는 위험프리미엄이 높아진다. 잉여소비비율 계산에 필요한 습관은 그 값을 관찰하기 힘들기 때문에 Wachter(2006)는 식 (10)과 같이 과거 10년간 분기별 소비증가율(Δc)로 잉여소비비율의 대용치(SURP)를 계산하고, 이를 실증분석에 사용하였다.

(10)SURPt=1−ψ1−ψ40∑j=039ψjΔc(t−j)

Santos and Veronesi(2006)는 투자자의 소비 재원이 근로소득과 금융자산의 배당으로 구성되는 경우, 소득의 구성비율이 변화하면 투자자가 요구하는 주식 혹은 금융자산의 위험 프리미엄(risk premium)도 변화한다고 설명하였다. 소비 재원 중 금융자산 배당의 비중이 낮아지면, 소비와 금융자산 수익률의 공분산이 작아지고 소비 CAPM에서 투자자가 요구하는 위험프리미엄이 낮아진다. 소비 대비 소득비율(Y / C)이 증가하면 투자자가 요구하는 위험자산 보유에 따른 위험 프리미엄이 감소하고 소비 대비 소득비율이 감소하면 위험 프리미엄이 증가하므로, 소비 대비 소득비율과 투자자가 요구하는 주식의 위험 프리미엄 또는 주식의 기대수익률은 음(-)의 관계에 있다. Park et al.(2019)은 자영업자의 근로소득 포함여부에 따라 두 가지 소비 대비 소득비율을 계산하였는데, 이중 자영업자의 근로소득을 포함한 경우 그 예측력의 통계적 유의성이 대체로 높게 나타났다.

상태변수로 사용할 소비관련 거시변수는 Park et al.(2019)이 제시한 변수 중 위험프리미엄에 대한 예측력이 높았던 변수를 사용한다. Lettau and Ludvigson(2001)의 총자산 대비 소비비율(consumption-aggregate wealth ratio; 이하 cay)은 Stock and Watson(1993)의 동적 회귀분석(dynamic least square)방법을 사용하여 소비, 자산 및 소득 등 세 변수 간의 공적분 관계식을 추정하고, 추정된 관계식으로부터 잔차를 계산하였다. 자산의 경우 비금융생산자산은 제외하고 금융자산만을 포함하였고, 소득에는 자영업자의 근로소득을 포함하였다. Campbell and Cochrane(1999)의 잉여소비비율(surplus consumption ratio; 이하 SURP)은 Wachter(2006)의 방법을 준용하여 10년간의 분기별 소비증가율로 그 대용치를 계산하였다. Santos and Veronesi(2006)의 소비 대비 소득비율(income to consumption ratio; 이하 Y / C)은 소득을 소비로 나누어 계산하였다. 소득의 계산에는 자영업자의 근로소득 포함하였다.

2.3 자료

자료 기간은 1991년 6월부터 2015년 12월까지 총 98분기이다. 포트폴리오의 분류를 위해서 1990년부터 일별 수정주가, 주식거래량, 상장주식수, 시가총액 그리고 자본금 등의 자료를 FnGuide에서 수집하였다. 상태변수는 이전 분기의 자료이며, 계산에는 전분기의 소비, 자산 및 소득 등의 자료가 필요하다. 거시변수 및 금리의 자료는 한국은행의 경제통계시스템에서 수집하였다.

횡단면 분석에 사용된 기업규모 및 장부가치 대 시장가치 비율의 16개 포트폴리오는 KOSPI에 포함되어 있는 비금융권 기업으로 구성하였다. 기업규모 및 장부가치 대 시장가치 비율의 두 가지 분류기준을 독립적으로 적용하기 때문에, 극단에 위치하는 포트폴리오는 적은 숫자의 주식이 포함되는 문제가 발생할 수 있어 25개 포트폴리오를 구성하는 대신 25% 비율로 구분하여 16개 포트폴리오를 구성하였다. 자본잠식상태인 기업을 제외하였으며, 표본기간 동안 평균적으로 약 597개의 주식을 분류하여 포트폴리오를 구성하였다. 분류기준인 기업규모와 장부가치 대 시장가치 비율은 전기말 대차대조표 자료³)와 4월 말의 시가총액을 기준으로 계산하고 5월부터 다음해 4월 말까지 포트폴리오 분류에 적용하였다.

강건성 검증에는 거래회전율과 기업 고유위험으로 각각 구분된 5분위 포트폴리오와 KOSPI의 산업별 포트폴리오 18개를 사용하였다. 거래회전율은 매월 일별 거래량을 해당일의 상장주식수로 나눈 값의 합계액으로 계산한 후 직전년 5월부터 해당년 4월까지 평균값을 계산하여 분류기준으로 사용하였다. 계산된 거래회전율을 사용하여 5월부터 다음해 4월까지의 포트폴리오를 구성하였다. 기업 고유위험은 매월 말 최근 2개월 간 거래가 30일 이상 있었던 주식에 대해 CAPM의 잔차(ε_i,t)를 계산하고 그 표준편차 값으로 추정하였다. 매월 말 계산된 고유위험의 추정치로 포트폴리오를 재분류하고, 한 달간의 수익률을 계산하였다. 잔차(ε_i,t)의 계산에는 Dimson(1979)의 비동기적 거래를 고려하기 위해 식 (11)의 Lewellen and Nagel (2006) 추정방법을 사용하였다. 거래회전율과 기업 고유위험으로 분류된 포트폴리오에 포함된 주식의 갯수의 평균값은 각각 약 587개와 628개이다.

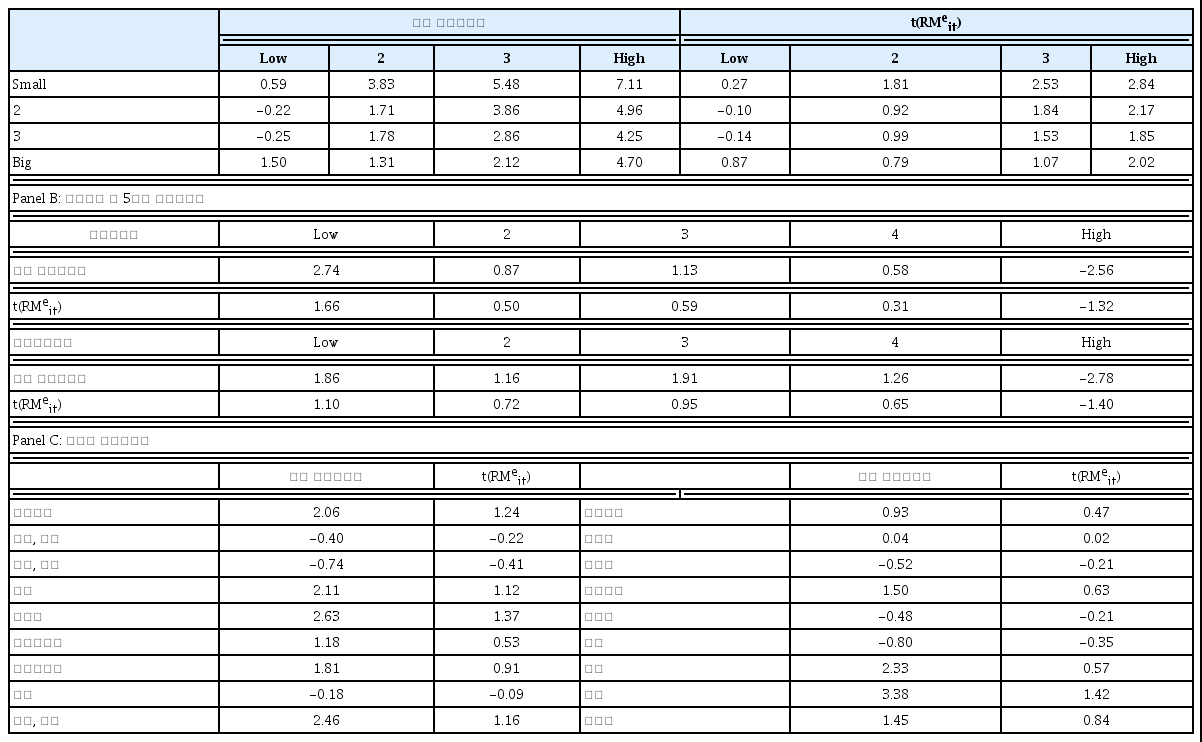
(11)Ri,te=αi+βi,0Rmt+βi,1Rmt−1+βi,2[Rmt−2+Rmt−3+Rmt−43]+εi,t

Ri,te 는 t기의 개별 주식의 일별 초과수익률을 의미하며, 주식거래가 없는 거래일의 가격을 제외하고 거래가 있는 거래일만의 가격으로 계산하였다.Rmt는 해당기간 종합주가지수(KOSPI)의 일별 초과수익률로 1년 만기 통안증권 금리를 사용하여 계산하였다. 해당기간 주식의 거래가 없는 경우 거래의 동기성을 맞추기 위하여Rmt의 계산에 이를 반영하였다. KOSPI의 산업별 포트폴리오의 수익률은 거래소의 KOSPI 산업별 지수 중 자료기간 전체에 지수가 존재하는 18개 산업별 지수를 사용하여 계산하였다.

기업규모와 장부가치 대 시장가치 비율의 16개 포트폴리오, 거래회전율 5분위 포트폴리오, 기업고유위험 5분위 포트폴리오 및 KOSPI 산업별 포트폴리오 18개 등 총 44개 포트폴리오의 월별 시가가중수익률(value weighted return)을 각각 계산하였다. 1년만기 통안증권 금리로 월간 초과수익률을 계산하고 이를 다시 분기 수익률로 변환하였다. <표 1>은 횡단면 분석에 사용된 개별 포트폴리오의 분기 초과수익률의 기초통계량이다. Panel A는 기업규모와 장부가치 대 시장가치의 두 가지 기준으로 분류된 포트폴리오의 초과수익률이다. 장부가치 대 시장가치 비율이 높은 가치주가 비율이 낮은 성장주에 비해 수익률이 대체로 높다. 소형주의 경우도 성장주의 경우를 제외하면 대체로 대형주보다 그 수익률이 높다. 성과가 가장 좋은 포트폴리오와 낮은 포트폴리오의 차이는 약 7.36%이다. Panel B는 5분위 포트폴리오의 초과수익률에 대한 기초통계량이다. 평균수익률의 패턴은 기존의 분석결과와 유사하게 나타났다. 거래회전율과 기업고유위험이 낮은 주식 포트폴리오의 초과수익률이 상대적으로 높다. 포트폴리오의 수익률 차이는 분류 기준별로 약 5.30%와 4.64%이다. Panel C는 산업별 포트폴리오의 분기별 초과수익률이다. 기간 중 보험업의 수익률이 가장 높았으며, 은행업의 수익률이 가장 낮다. 두 포트폴리오의 수익률 차이는 약 4.18%이다.

<표 1>

주식 포트폴리오의 초과수익률

분석에 사용한 포트폴리오의 분기 초과수익률의 기초통계량이다. Panel A는 기업규모(size) 및 장부가치 대 시장가치(book to market) 비율로 구분한 16개 포트폴리오의 기초통계량이다. 두 가지 분류기준을 독립적으로 적용하여 25% 단위로 16개 포트폴리오를 구성하였다. 기업규모와 장부가치 대 시장가치 비율은 전기 말 대차대조표 자료와 4월 말 시가총액을 기준으로 계산하고 5월부터 다음해 4월말까지의 포트폴리오 분류에 적용하였다. Panel B는 거래회전율(turnover)과 기업의 고유위험 (idiosyncratic risk)으로 구분된 5분위 포트폴리오 10개를 분류기준 별로 작은 기업에서 큰 기업으로 순으로 표시하였다. 거래회전율은 매월 일별 거래량을 해당일의 상장주식수로 나눈 값의 합계액으로 계산한 후 직전년 5월부터 해당년 4월까지 평균값을 계산하여 분류기준으로 사용하였다. 계산된 거래회전율을 사용하여 5월부터 다음해 4월까지의 포트폴리오를 구성하였다. 기업 고유위험은 매월 말 최근 2개월간 거래가 30일 이상 있었던 주식에 대해 CAPM의 잔차를 계산하고 그 표준편차 값으로 추정하였다. 매월 말 다음 한 달간의 포트폴리오를 재분류하였다. Panel A와 B의 포트폴리오는 KOSPI에 포함되어 있는 비금융권 기업으로 구성하였다. Panel C는 KOSPI의 산업별 포트폴리오 분기별 초과수익률에 대한 기초통계량이다. 자료기간은 1991년 6월부터 2015년 12월까지이며, 총 98분기이다.

Panel A: 기업규모와 장부가치 대 시장가치를 기준으로 분류한 포트폴리오

실증분석에 사용된 자산가격모형의 위험요인은 MKT(주가지수 초과수익률), SMB(기업규모 위험 모방 포트폴리오), HML(장부가치 대 시장가치 위험 모방 포트폴리오), (소득증가율) 및(소비증가율)이고, 시간가변적 위험프리미엄을 반영하기 위한 상태변수는 cay(총자산 대비 소비비율), SURP(잉여소비비율) 및 Y / C (소비 대비 소득비율)이다.

MKT는 종합주가지수(KOSPI)와 1년 만기 통안증권 금리로 월 초과수익률을 계산하고, 이를 다시 분기 수익률로 변환하였다. 종합주가지수는 현금배당을 포함하지 않기 때문에 이를 반영하기 위해 2000년 이전의 기간은 증권통계연보의 배당수익률 자료를, 이후 기간은 한국은행 경제통계시스템의 KOSPI 배당수익률 자료를 사용하였다. 시가가중 배당수익률 자료는 최근 12개월간 배당의 합을 시가총액으로 나눈 값으로, 매년 12월 수익률에 배당수익률을 더해주는 방법으로 배당이 포함된 월별 초과수익률을 계산하였다.

SMB와 HML은 Hahn and Yoon(2016)의 방법을 준용하여 계산하였다. 기업규모 및 장부가치 대 시장가치 비율의 두 가지 분류기준을 독립적으로 적용하여 3:4:3 비율의 9가지 포트폴리오를 구성하고 각 포트폴리오 별로 시가가중수익률을 계산하였다. SMB는 기업규모 하위 3개 포트폴리오의 평균수익률에서 상위 3개 포트폴리오의 평균수익률을 차감하여 계산하였고, HML은 장부가치 대 시장가치 비율 상위 3개 포트폴리오의 평균수익률에서 하위 3개 포트폴리오의 평균수익률을 차감하여 계산하였다.

모형의 위험요인 중 소득증가율(Δy) 및 소비증가율(Δc) 그리고 세 가지 상태변수의 계산에는 소비, 자산 및 소득에 대한 자료가 필요하다. 소비는 가계의 소비자료 중 비내구재와 서비스에 대한 최종소비지출의 합계로 계산하였다. 개인소비지출 디플레이터(PCE deflator)의 계산은 비내구재와 서비스에 대한 계절조정 최종소비지출의 명목금액 합계액과 실질금액 합계액을 사용하였다.

자산은 cay의 계산에 필요한 변수로, 금융자산만을 포함하여 계산한 cay의 예측력이 비금융생산자산을 포함하는 경우 보다 높았기 때문에 자산에는 금융자산만을 포함하였다. 금융자산은 한국은행의 분기별 자금순환표에서 가계 및 비영리단체의 자산총액에서 부채총액을 차감하여 계산하였다. 자금순환표의 금융자산부채 잔액표는 1968년 SNA, 1993년 SNA 및 2008년 SNA 기준의 세 가지 시계열이 존재한다. 현재 기준이 되고 있는 2008년 SNA 기준의 자료는 2008년 4분기부터 존재한다. 최근의 SNA 기준으로 만든 자료를 우선으로 사용하되, 이전의 SNA 기준으로 만들어진 자료를 연속성이 유지되도록 값을 조정하여 사용하였다. 1993년 SNA 기준 자료는 시작 시점인 2002년 4분기부터 2008년 SNA 기준 자료가 존재하지 않는 2008년 3분기까지의 총 24분기 자료에 대해 2008년 4분기 두 SNA 기준의 자료 값의 차이 3.6%를 각 분기별 추가 증가율이 같도록 배분하였다. 같은 방법으로 1968년 SNA 기준의 1975년 1분기부터 2002년 3분기까지의 자료에 대해서도 조정하였다. 조정비율은 각 분기별로 2008년 3분기 이전기간은 약 0.15%이고, 2002년 3분기 이전기간은 약 0.14%이다.

소득은 임금 및 급여 그리고 고용주의 사회부담금을 포함하는 피용자보수에 사회수혜금을 더하고 가계의 사회부담금과 세금을 차감하여 계산하였다. Gollin(2002)과 Kim(2013)은 국가별 노동소득 분배율의 차이를 전체 취업자 중 자영업자 비중의 차이로 설명하였는데, 자영업자의 비중이 높거나 변화하는 경우 소득의 측정에 오류가 있을 수 있다. 자영업자의 소득은 개인 및 비영리단체의 영업잉여 항목에 계상되어 있는데, 영업잉여는 자본과 노동에 대한 소득을 모두 포함한다. 따라서 개인 및 비영리단체의 영업소득에 일반기업의 근로소득 분배율을 적용하여 자영업자의 근로소득을 계산한 후 이를 소득 계산에 포함하였다. 국민총소득(GNI)은 분기별 자료이지만, 계산에 필요한 국민처분가능소득의 세부항목은 연간 자료만 존재하기 때문에 연단위로 소득을 계산한 후 분기별 계절조정 명목 국민총소득(GNI)의 누적액이 해당년도의 소득 금액과 일치하는 연도별 비율을 매년 계산하여 분기별 소득을 계산하였다. 각각의 자료를 인구수와 개인소비지출 디플레이터로 나누어 1인당 실질 소비, 자산 그리고 소득을 계산하고 이를 이용하여 소득증가율, 소비증가율 그리고 소비관련 거시변수를 계산하였다.

<표 2>는 횡단면 분석에 사용된 개별 위험요인들과 상태변수의 기초 통계량이다. 상태변수는 1분기 이전의 자료이다. 소형주가 대형주에 비해 평균수익률이 높고, 가치주가 성장주 대비 평균수익률이 높으므로, SMB와 HML의 평균값은 양수이다. SMB와 HML의 상관계수는 음(-)의 값이며, 소비증가율과 소득증가율의 상관계수가 0.57로 높게 나타났다. 상태변수 간에 상관계수는 SURP와 Y / C의 값이 0.82로 높게 나타났으며, cay와 SURP의 상관계수 값은 0.04로 낮았다. 세 가지 소비관련 거시변수와 MKT의 상관계수는 모두 상대적으로 낮은 음(-)의 값(-0.01~-0.13)을 보여주고 있다.

<표 2>

자료의 기초통계량

분석에 사용한 자료의 기초통계량이다. 종합주가지수(KOSPI)의 분기 초과수익률(MKT)은 배당수익률을 포함한 종합주가지수 수익률에서 1년 만기 통안증권 금리를 차감하여 계산하였다. 기업규모 위험의 모방 포트폴리오(SMB)와 장부가치 대 시장가치 위험 모방 포트폴리오(HML)의 수익률 계산은 Hahn and Yoon(2016)의 방법을 준용하여, 종합주가지수에 포함되어 있는 비금융권 기업을 기업규모 (size)와 장부가치 대 시장가치(book to market)를 기준으로 3:4:3 비율로 분류된 9개의 포트폴리오를 사용하였다. SMB는 기업규모 하위 3개 포트폴리오의 평균수익률에서 상위 3개 포트폴리오의 평균수익률을 차감하여 계산하였고, HML은 장부가치 대 시장가치 상위 3개 포트폴리오의 평균수익률에서 하위 3개 포트폴리오의 평균수익률을 차감하여 계산하였다. 와 는 각각 자영업자의 수익을 포함한 1인당 실질소득, 그리고 1인당 실질소비의 분기별 증가율이다. 사용된 자료의 표본기간은 1991년 6월부터 2015년 12월까지 총 98분기이다. 조건부 모형의 상태변수(SV_t-1)로 소비관련 거시변수 cay, SURP 및 Y / C의 분기자료를 사용하였다. cay는 Lettau and Ludvigson(2001)의 cay를 소비, 금융자산 및 자영업자를 포함한 노동소득으로 계산한 값이다. SURP는 Campbell and Cochrane(1999)의 잉여소비비율의 대용치인 Wachter(2006)의 잉여소비비율이고, Y / C는 Santos and Veronesi(2006)의 소비 대비 소득비율로 소비와 자영업자를 포함한 노동소득으로 계산하였다. 조건부 변수로 사용된 cay, SURP 및 Y / C는 1분기 이전의 자료이다. 상관계수의 우측상단에 표기된 ^*는 10%, ^**는 5%, 그리고 ^***는 1% 수준에서 통계적 유의성을 표시한다.

3. 분석결과

3.1 분석대상: 16개 포트폴리오

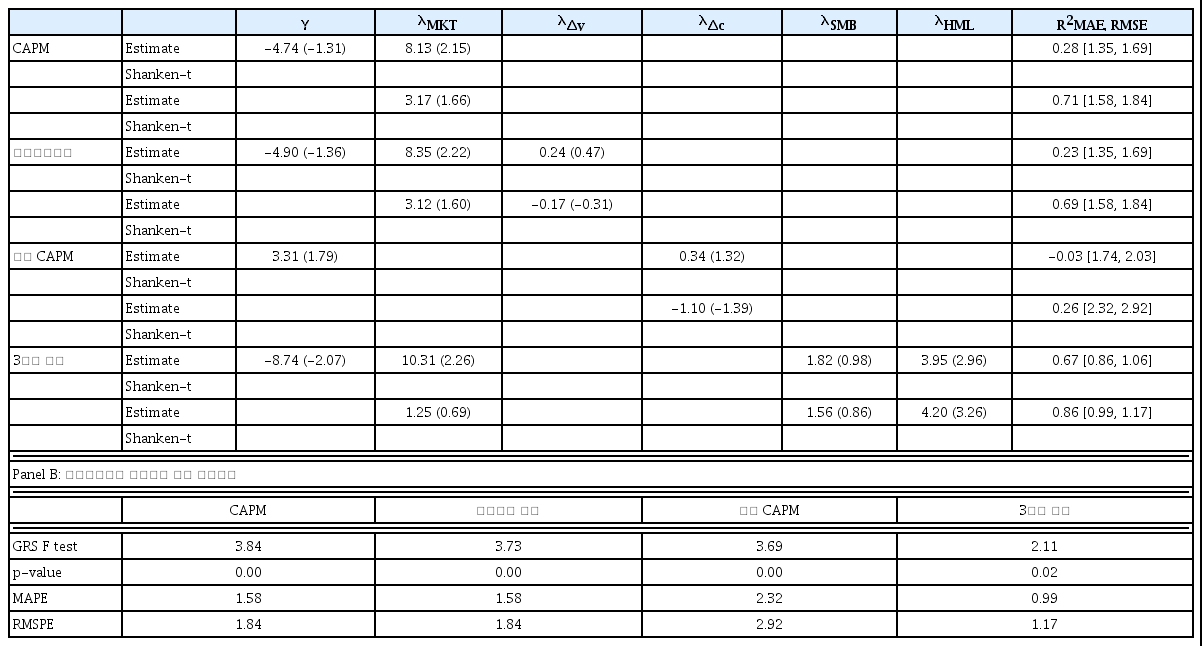
횡단면 분석은 Fama and MacBeth(1973)의 시계열 회귀분석 및 횡단면 회귀분석의 2단계 추정방법을 사용하였다. 분석에 사용된 포트폴리오는 기업규모 및 장부가치 대 시장가치의 두 가지 기준으로 분류된 16개 포트폴리오이다. <표 3>은 기본모형 또는 비조건부모형의 횡단면 분석결과로 Panel A는 2단계 회귀분석으로 추정한 위험프리미엄(λ)과 Shanken (1992)의 표준오차에 의한 t값을 표시하였다. 실증분석에서 16개 포트폴리오의 초과수익률을 사용하고 위험요인이 포트폴리오인 경우는 초과수익률을 거시변수인 경우에는 시계열 회귀분석의 상수항이 0이 되도록 위험요인을 조정해 주었기 때문에, 모형의 설명력이 높다면 시계열 회귀분석의 상수항과 횡단면 회귀분석의 상수항은 0이 되어야 한다. 횡단면 실증분석의 효율성과 강건성 측면에서 식 (4)의 횡단면 분석의 상수항(γ)이 0이라는 제약 여부에 따라 자산가격모형별로 2가지 경우의 위험프리미엄을 모두 추정하였다. 상수항(γ)이 0이라는 제약 조건이 없는 경우, MKT의 위험프리미엄 추정치는 CAPM, 인적자본 모형 및 3요인 모형에서 모두 5% 수준에서 통계적으로 유의한 양(+)의 값을 보여준다. 하지만 상수항(γ)을 0으로 제약하는 경우, MKT 위험프리미엄 추정치는 모두 통계적으로 유의하지 않다. 인적자본 모형의 소득증가율(Δy)과 소비 CAPM의 소비증가율(Δc)의 위험프리미엄 추정치는 제약 여부와 상관 없이 통계적으로 유의하지 않다. 3요인 모형의 경우 SMB의 위험프리미엄 추정치는 유의하지 않지만, HML의 추정치는 통계적으로 유의하며 상수항(γ)이 0이라는 제약을 한 경우 MKT와 HML의 위험프리미엄 값이 각각 1.25와 4.20로 <표 2>의 평균값과 유사하게 나타났다.

<표 3>

비조건부 모형 분석결과(16개 포트폴리오)

4가지 비조건부 모형을 기업규모(size)와 장부가치 대 시장가치(book to market) 비율로 분류된 16개 포트폴리오를 사용하여 분석한 결과이다. 분석기간은 1991년 6월부터 2015년 12월까지 총 98분기이다. Panel A는 Fama and MacBeth(1973)의 방법을 이용한 횡단면 분석 결과이다. 횡단면 분석의 상수항(γ)이 0이라는 제약 여부에 따라 모형별로 2가지 위험프리미엄(λ)의 추정값과 Shanken(1992)의 표준오차에 의한 t값을 표시하였다. Jagannathan and Wang(1996)의 조정된 결정계수(adjusted R²)와 꺽쇠괄호 안에 횡단면 회귀분석의 평균절대오차(MAE)와 평균제곱근오차(RMSE)를 표시하였다. Panel B는 시계열분석의 ‘개별 포트폴리오의 상수항이 모두 0이다.’라는 귀무가설의 검정을 위한 Gibbons, Ross, and Shanken(1989)의 GRS F값과 그 유의수준을 표시하였다. MAPE는 개별 포트폴리오별 상수항의 절대값에 대한 평균이고, RMSPE는 포트폴리오별 상수항 제곱의 평균을 다시 제곱근한 값이다.

Panel A: 위험프리미엄(λ)의 추정 결과

모형별로 Jagannathan and Wang(1996)의 조정된 결정계수(R²) 값을 살펴보면 3요인 모형의 조정된 결정계수 값이 제일 높고 CAPM과 인적자본 모형의 조정된 결정계수 값은 유사한 수준이며 소비 CAPM의 조정된 결정계수 값이 제일 낮게 나타났다. 횡단면 분석의 오차를 나타내는 평균절대오차(MAE) 값과 평균제곱근오차(RMSE) 값의 경우 3요인 모형이 제일 작고, 소비 CAPM이 제일 크게 나타나 조정된 결정계수, MAE와 RMSE 값에 따른 모형의 설명력은 3요인 모형이 가장 우수하고, 소비 CAPM이 상대적으로 낮은 것으로 해석이 가능하다.

시계열 회귀분석의 상수항에 대한 통계량은 Panel B에 표시하였다 ‘개별 포트폴리오의 상수항이 모두 0이다.’라는 귀무가설에 대한 GRS-F 검증 결과 4개의 모형 모두 5% 유의수준에서 기각되는 결과를 보여준다. MAPE는 포트폴리오별 상수항의 절대값에 대한 평균값이고, RMSPE는 포트폴리오별 상수항 제곱의 평균을 다시 제곱근한 값으로, 3요인 모형의 값이 다른 모형에 비해 상대적으로 작게 나타나 횡단면 분석과 시계열 분석 모두 비조건부 모형 중에서는 3요인 모형의 설명력이 상대적으로 높다고 해석할 수 있다.

조건부 자산가격모형은 식 (3)과 같이 비조건부모형으로 표시할 수 있으므로, Fama and MacBeth(1973)의 방법으로 동일하게 추정하였다. 조건부모형은 이전 분기의 세 가지 소비관련 거시변수를 상태변수(SV_t-1)로 사용하였다. 상태변수는 비교의 편의를 위해 평균이 0이고 표준편차가 1이 되도록 조정하였다. <표 4>의 결과를 보면 조건부 CAPM의 추정결과에서 조건부모형의 조정된 결정계수, MAE와 RMSE 값은 비조건부모형에 비해 개선되었다. cay를 상태변수로 사용하는 경우 상수항(γ)이 0이라는 제약 조건이 없는 경우는 상태변수의 위험프리미엄(λ_SV) 추정치는 10% 수준에서 통계적으로 유의하고, 제약조건이 있는 경우, 상태변수와 시장위험의 교차 위험프리미엄(λ_SV·MKT) 추정치가 통계적으로 유의하다. 상태변수가 SURP인 경우 제약조건이 있는 경우에만 상태변수와 시장위험의 교차 위험프리미엄(λ_SV·MKT) 추정치가 통계적으로 유의하다. 상태변수가 Y/C 인 경우 상태변수와 시장위험의 교차 위험프리미엄(λ_SV·MKT) 추정치가 상수항에 대한 제약조건 여부와 상관없이 모두 통계적으로 유의하게 나타났다. Panel B의 결과를 보면 상태변수가 cay인 경우 MAPE와 RMSPE 값이 가장 작게 나타났다. <표 4>의 결과를 종합적으로 요약하면 조건부 CAPM의 분석결과 비조건부 모형에 비해 전체적인 설명력이 향상되었으며, 특히 상태변수가 cay와 Y / C인 경우 모형의 설명력이 SURP를 사용한 경우에 대비 높게 나타났다.

<표 4>

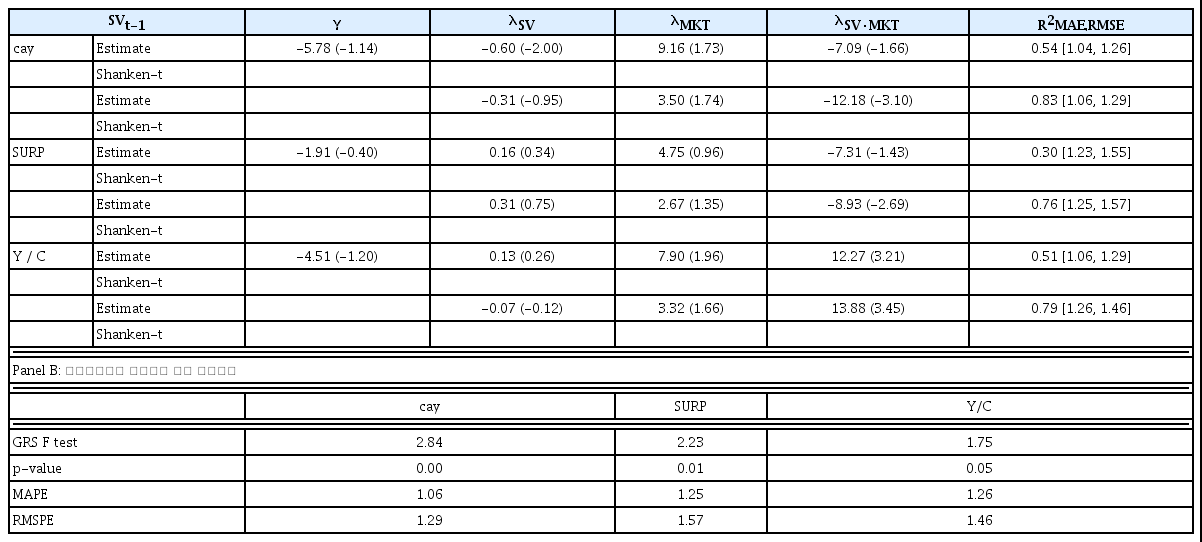
조건부 CAPM 분석결과(16개 포트폴리오)

조건부 CAPM의 식 Rite = λ₀ + λ_SV β_SV + λ_MKT β_MKT + λ_SV·MKT β_SV·MKT + ν_it 을 기업규모(size)와 장부가치 대 시장가치(book to market) 비율로 분류된 16개 포트폴리오를 사용하여 분석한 결과이다. 분석기간은 1991년 6월부터 2015년 12월까지 총 98분기이다. Panel A는 Fama and MacBeth(1973)의 방법을 이용한 횡단면 분석 결과이다. 횡단면 분석의 상수항(γ)이 0이라는 제약 여부에 따라 모형별로 2가지 위험프리미엄(λ)의 추정값과 Shanken(1992)의 표준오차에 의한 t값을 표시하였다. Jagannathan and Wang(1996)의 조정된 결정계수(adjusted R²)와 꺽쇠괄호 안에 횡단면 회귀분석의 평균절대오차(MAE)와 평균제곱근오차(RMSE)를 표시하였다. Panel B는 시계열분석의 ‘개별 포트폴리오의 상수항이 모두 0이다.’라는 귀무가설의 검정을 위한 Gibbons et al.(1989)의 GRS F값과 그 유의수준을 표시하였다. MAPE는 개별 포트폴리오별 상수항의 절대값에 대한 평균이고, RMSPE는 포트폴리오별 상수항 제곱의 평균을 다시 제곱근한 값이다.

Panel A: 위험프리미엄(λ)의 추정 결과

<표 5>는 조건부 인적자본 모형의 추정결과이다. 상태변수가 cay인 경우 조정된 결정계수의 값이 0.68과 0.89로 3요인 모형의 조정된 결정계수 값 0.67과 0.86 보다 높게 나타났으며, MAE와 RMSE 값도 3요인 모형의 값보다 작다. 상태변수와 소득증가율의 교차 위험프리미엄(λ_SV·ρy) 추정치는 상수항에 대한 제약조건이 있는 경우 유의적이며, Panel B의 MAPE 및 RMSPE 값도 3요인 모형의 값보다 작다. 상태변수가 SURP와 Y / C인 경우 상태변수와 시장위험의 교차 위험프리미엄(λ_SV·MKT)의 추정치가 통계적으로 유의하며, 비조건부 모형에 비해 모형의 설명력이 향상되었다. 상태변수로 cay와 Y / C를 사용하는 경우의 설명력 향상이 상대적으로 크다.

<표 5>

조건부 인적자본 모형 분석결과(16개 포트폴리오)

조건부 인적자본 모형의 식 Rite = λ_o + λ_sv β_sv + λ_MKT β_MKT + λ_Δy β _Δy + λ_SV·MKT β_SV·MKT + λ_SV ·_Δy β_SV · _Δy + v_it 을 기업규모(size)와 장부가치 대 시장가치(book to market) 비율로 분류된 16개 포트폴리오를 사용하여 분석한 결과이다. 분석기간은 1991년 6월부터 2015년 12월까지 총 98분기이다. Panel A는 Fama and MacBeth(1973)의 방법을 이용한 횡단면 분석 결과이다. 횡단면 분석의 상수항(γ)이 0이라는 제약 여부에 따라 모형별로 2가지 위험프리미엄(λ)의 추정값과 Shanken(1992)의 표준오차에 의한 t값을 표시하였다. Jagannathan and Wang(1996)의 조정된 결정계수(adjusted R²)와 꺽쇠괄호 안에 횡단면 회귀분석의 평균절대오차(MAE)와 평균제곱근오차(RMSE)를 표시하였다. Panel B는 시계열분석의 ‘개별 포트폴리오의 상수항이 모두 0이다.’라는 귀무가설의 검정을 위한 Gibbons et al.(1989)의 GRS F값과 그 유의수준을 표시하였다. MAPE는 개별 포트폴리오별 상수항의 절대값에 대한 평균이고, RMSPE는 포트폴리오별 상수항 제곱의 평균을 다시 제곱근한 값이다.

Panel A: 위험프리미엄(λ)의 추정 결과

<표 6>은 조건부 소비 CAPM의 분석결과이다. 상태변수가 cay인 경우 상태변수와 소득증가율의 교차 위험프리미엄(λ_SV·ρc)의 추정치가 상수항에 대한 제약조건 여부와 상관없이 통계적으로 유의하다. 상태변수가 Y / C인 경우는 상수항에 대한 제약조건이 없는 경우에만 상태변수의 위험프리미엄(λ_SV)과 상태변수와 소득증가율의 교차 위험프리미엄(λ_SV·ρc)의 추정치가 통계적으로 유의하며, Panel B에서 MAPE와 RMSPE 값이 조건부 소비 CAPM 중 가장 작다.

<표 6>

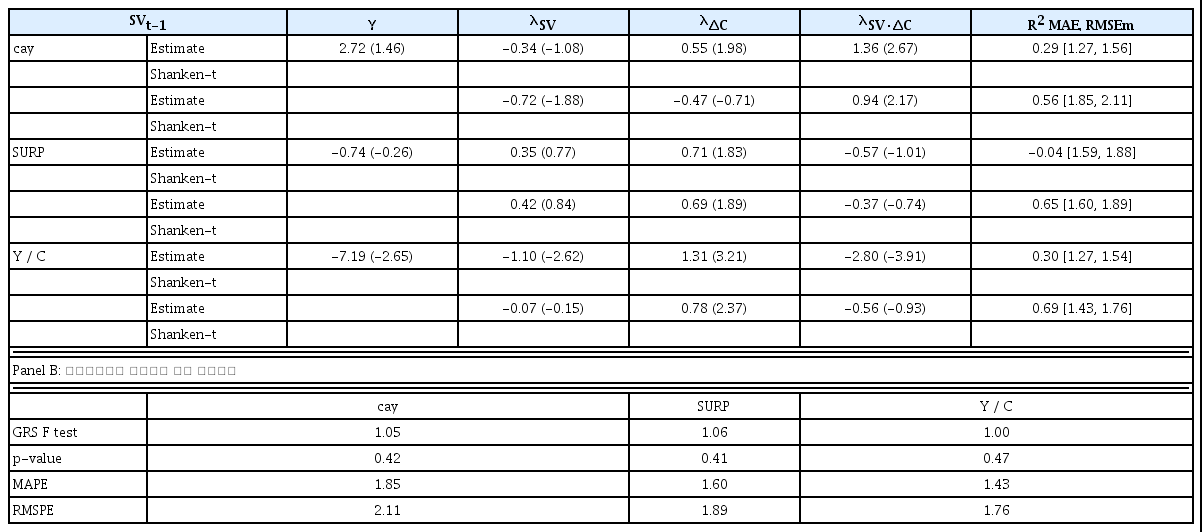
조건부 소비 CAPM 분석결과(16개 포트폴리오)

조건부 소비 CAPM 식 Rite = λ_o + λ_SV β_SV + λ_Δc β_Δc + λ_SV · _Δc β_SV · _Δc + v_it을 기업규모(size)와 장부가치 대 시장가치(book to market) 비율로 분류된 16개 포트폴리오를 사용하여 분석한 결과이다. 분석기간은 1991년 6월부터 2015년 12월까지 총 98분기이다. Panel A는 Fama and MacBeth(1973)의 방법을 이용한 횡단면 분석 결과이다. 횡단면 분석의 상수항(γ)이 0이라는 제약 여부에 따라 모형별로 2가지 위험프리미엄(λ)의 추정값과 Shanken(1992)의 표준오차에 의한 t값을 표시하였다. Jagannathan and Wang(1996)의 조정된 결정계수(adjusted R²)와 꺽쇠괄호 안에 횡단면 회귀분석의 평균절대오차(MAE)와 평균제곱근오차(RMSE)를 표시하였다. Panel B는 시계열분석의 ‘개별 포트폴리오의 상수항이 모두 0이다.’라는 귀무가설의 검정을 위한 Gibbons, Ross, and Shanken(1989)의 GRS F값과 그 유의수준을 표시하였다. MAPE는 개별 포트폴리오별 상수항의 절대값에 대한 평균이고, RMSPE는 포트폴리오별 상수항 제곱의 평균을 다시 제곱근한 값이다.

Panel A: 위험프리미엄(λ)의 추정 결과

<표 7>은 조건부 3요인 모형의 분석결과이다. 3요인 모형의 조건부 모형은 MKT의 계수만을 소비관련 거시변수의 선형함수로 가정하였다. 상태변수가 cay인 경우 조정된 결정계수, MAE와 RMSE가 개선되었으며, 상수항에 대한 제약조건이 있는 경우에만 상태변수와 시장위험의 교차 위험프리미엄(λ_SV·MKT)의 추정치가 통계적으로 유의하다. 상태변수가 Y / C인 경우도 조정된 결정계수, MAE와 RMSE가 개선되었으며, 상수항에 대한 제약조건 여부와 관계없이 상태변수와 시장위험의 교차 위험프리미엄(λ_SV·MKT)의 추정치가 통계적으로 유의하다.

<표 7>

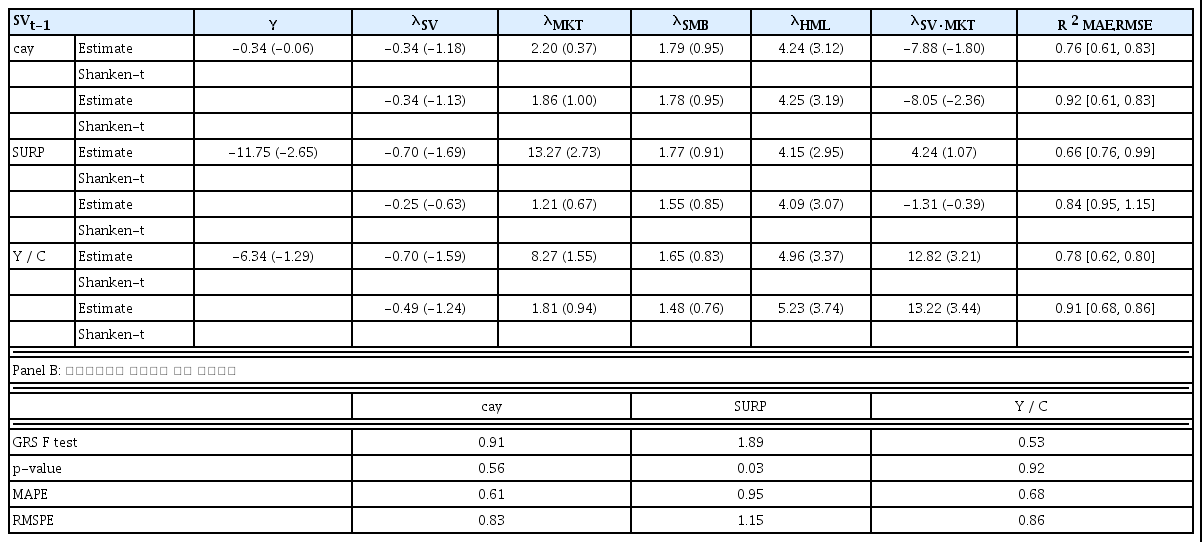
조건부 3요인 모형 분석결과(16개 포트폴리오)

3요인 모형의 위험요인 중 MKT의 계수를 소비관련 거시변수의 선형함수로 가정한 3요인 모형의 식 Rite = λ_o + λ_SV β_SV + λ_MKT β_MKT + λ_SMB β_SMB + λ_HML β_HML + λ_SV·MKT β_SV·MKT + V_it 을 기업규모(size)와 장부가치 대 시장가치(book to market) 비율로 분류된 16개 포트폴리오를 사용하여 분석한 결과이다. 분석기간은 1991년 6월부터 2015년 12월까지 총 98분기이다. Panel A는 Fama and MacBeth(1973)의 방법을 이용한 횡단면 분석 결과이다. 횡단면 분석의 상수항(γ)이 0이라는 제약 여부에 따라 모형별로 2가지 위험프리미엄(λ)의 추정값과 Shanken(1992)의 표준오차에 의한 t값을 표시하였다. Jagannathan and Wang(1996)의 조정된 결정계수(adjusted R²)와 꺽쇠괄호 안에 횡단면 회귀분석의 평균절대오차(MAE)와 평균제곱근오차(RMSE)를 표시하였다. Panel B는 시계열분석의 ‘개별 포트폴리오의 상수항이 모두 0이다.’라는 귀무가설의 검정을 위한 Gibbons, Ross, and Shanken(1989)의 GRS F값과 그 유의수준을 표시하였다. MAPE는 개별 포트폴리오별 상수항의 절대값에 대한 평균이고, RMSPE는 포트폴리오별 상수항 제곱의 평균을 다시 제곱근한 값이다.

Panel A: 위험프리미엄(λ)의 추정 결과

<표 4>, <표 5>, <표 6>, <표 7>에 보고된 기업규모와 장부가치 대 시장가치로 분류된 16개 포트폴리오를 대상으로 한 실증분석의 결과에서 세 가지 소비관련 거시변수를 상태변수로 사용한 조건부모형은 비조건부모형에 비해 대체로 조정된 결정계수가 향상되고 MAE, RMSE, MAPE 및 RMSPE 값도 개선되었다. 특히 조건부 인적자본 모형의 설명력은 조건부 CAPM, 조건부 소비 CAPM에 비해 높게 나타났으며 Fama and French(1993)의 3요인 모형과 유사한 수준의 설명력을 보여주었다. 3요인 모형에 상태변수를 사용하는 경우에도 그 설명력이 향상되는 결과를 얻을 수 있었다. 따라서 소비관련 거시변수가 3요인 모형의 세 가지 위험요인이 설명하지 못하는 주식수익률의 횡단면적 차이에 대한 설명력을 가지고 있다고 유추해 볼 수 있다.

3.2 분석대상: 44개 포트폴리오

강건성 검증을 위해 Lewellen et al.(2010)의 제안에 따라 분석의 대상 포트폴리오를 확장하였다. 분석에 사용된 포트폴리오는 기업규모와 장부가치 대 시장가치 비율로 분류한 포트폴리오 16개, 주식 거래회전율 및 기업 고유위험으로 분류된 5분위 포트폴리오 10개 및 KOSPI 산업별 포트폴리오 18개 등 총 44개 포트폴리오이다. <표 8>은 비조건부모형의 횡단면 분석결과이다. MKT의 위험프리미엄 추정치는 CAPM, 인적자본 모형, 3요인 모형 모두 유의하지 않게 나타났다. 포트폴리오를 확장하면서 인적자본 모형의 소득증가율(Δy)의위험프리미엄이 통계적으로 유의하게 나타났지만, 소비 CAPM의 소비증가율(Δc)의 위험 프리미엄 추정치는 통계적으로 유의하지 않다. 3요인 모형의 경우 HML의 추정치는 포트폴리오 확장여부와 상관 없이 통계적으로 유의하다. 포트폴리오가 확장되면서 조정된 결정계수의 값이 모두 낮아지고, MAE와 RMSE의 값은 증가하였다. Panel B에서 CAPM과 3요인 모형의 MAPE 및 RMSPE의 값은 증가하였지만, 인적자본 모형과 소비 CAPM의 경우는 감소하였다.

<표 8>

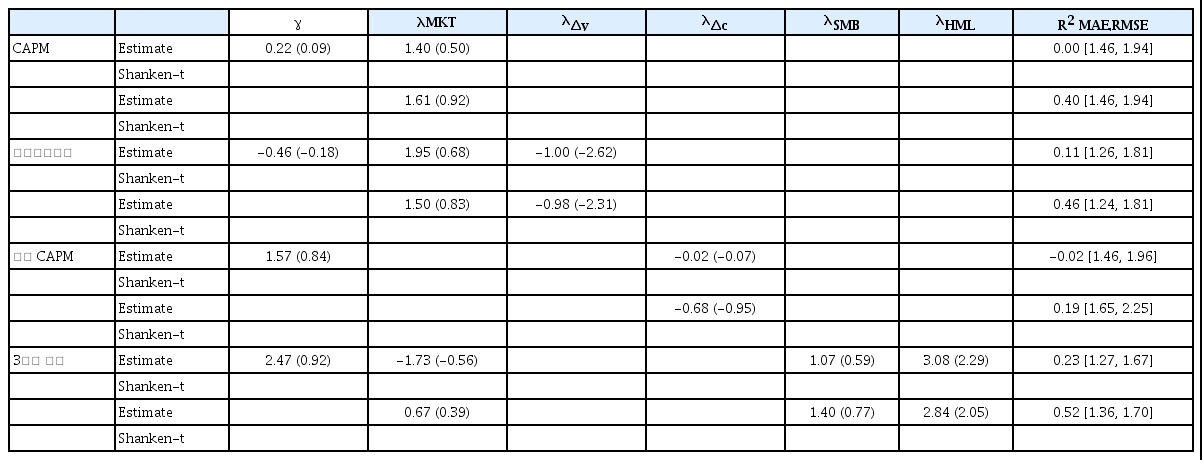
비조건부 모형 분석결과(44개 포트폴리오)

4가지 비조건부 모형을 기업규모(size)와 장부가치 대 시장가치(book to market) 비율로 분류된 16개 포트폴리오, 주식거래 회전율(turnover) 그리고 기업 고유위험(idiosyncratic risk)으로 분류한 5분위 포트폴리오 10개 포트폴리오 및 KOSPI의 산업별 포트폴리오 18개를 사용하여 분석한 결과이다. 분석기간은 1991년 6월부터 2015년 12월까지 총 98분기이다. Panel A는 Fama and MacBeth(1973)의 방법을 이용한 횡단면 분석 결과이다. 횡단면 분석의 상수항(γ)이 0이라는 제약 여부에 따라 모형별로 2가지 위험프리미엄(λ)의 추정값과 Shanken(1992)의 표준오차에 의한 t값을 표시하였다. Jagannathan and Wang(1996)의 조정된 결정계수(adjusted R²)와 꺽쇠괄호 안에 횡단면 회귀분석의 평균절대오차(MAE)와 평균제곱근오차(RMSE)를 표시하였다. Panel B는 시계열분석의 ‘개별 포트폴리오의 상수항이 모두 0이다.’라는 귀무가설의 검정을 위한 Gibbons, Ross, and Shanken(1989)의 GRS F값과 그 유의수준을 표시하였다. MAPE는 개별 포트폴리오별 상수항의 절대값에 대한 평균이고, RMSPE는 포트폴리오별 상수항 제곱의 평균을 다시 제곱근한 값이다.

Panel A: 위험프리미엄(λ)의 추정 결과

Panel B: 시계열분석의 상수항에 대한 분석결과

<표 9>의 조건부 CAPM의 추정결과에서 상태변수로 SURP를 사용한 경우 상태변수의 위험프리미엄(λ_SV) 추정치가 상수항에 대한 제약조건과 관계없이 통계적으로 유의하게 나타났다. 상태변수를 사용한 조건부모형의 조정된 결정계수, MAE, RMSE 값이 비조건부모형에 비해 개선되었다. Panel B의 MAPE와 RMSPE 값도 비조건부모형에 비해 개선되었으며, SURP를 사용한 경우가 가장 낮게 나타났다.

<표 9>

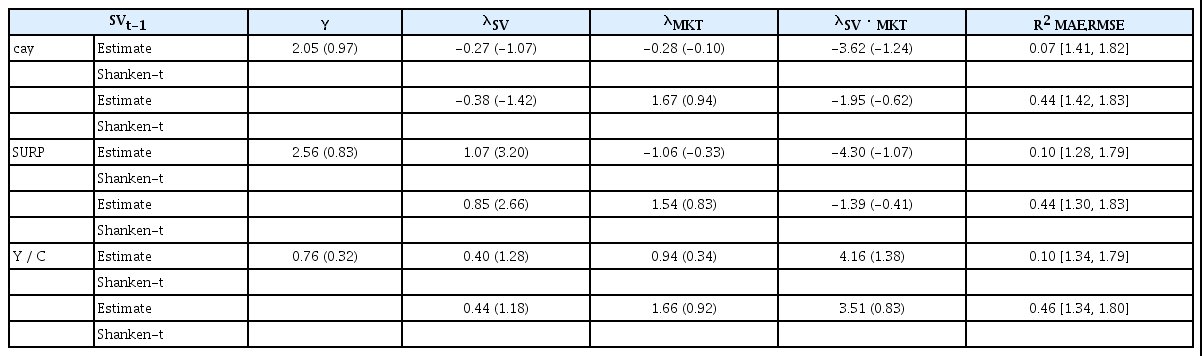
조건부 CAPM 분석결과(44개 포트폴리오)

조건부 CAPM의 식 Rite = λ_o λ_SV β_SV + λ_MKT β_MKT + λ_SV·MKT β_SV·MKT + v_it 을 4가지 비조건부 모형을 기업규모(size)와 장부가치 대 시장가치(book to market) 비율로 분류된 16개 포트폴리오, 주식거래 회전율(turnover) 그리고 기업 고유위험(idiosyncratic risk)으로 분류한 5분위 포트폴리오 10개 포트폴리오 및 KOSPI의 산업별 포트폴리오 18개를 사용하여 분석한 결과이다. 분석기간은 1991년 6월부터 2015년 12월까지 총 98분기이다. Panel A는 Fama and MacBeth(1973)의 방법을 이용한 횡단면 분석 결과이다. 횡단면 분석의 상수항(γ)이 0이라는 제약 여부에 따라 모형별로 2가지 위험프리미엄(λ)의 추정값과 Shanken(1992)의 표준오차에 의한 t값을 표시하였다. Jagannathan and Wang(1996)의 조정된 결정계수(adjusted R²)와 꺽쇠괄호 안에 횡단면 회귀분석의 평균절대오차(MAE)와 평균제곱근오차(RMSE)를 표시하였다. Panel B는 시계열분석의 ‘개별 포트폴리오의 상수항이 모두 0이다.’라는 귀무가설의 검정을 위한 Gibbons et al.(1989)의 GRS F값과 그 유의수준을 표시하였다. MAPE는 개별 포트폴리오별 상수항의 절대값에 대한 평균이고, RMSPE는 포트폴리오별 상수항 제곱의 평균을 다시 제곱근한 값이다.

Panel A: 위험프리미엄(λ)의 추정 결과

Panel B: 시계열분석의 상수항에 대한 분석결과

<표 10>의 조건부 인적자본 모형의 추정결과에서는 상태변수가 cay이고 상수항에 대한 제약이 없는 경우의 상태변수와 소득증가율의 교차 위험프리미엄(λ_SV·ρy) 추정치가 통계적으로 유의하고 조정된 결정계수의 값이 0.33과 0.57로 3요인 모형의 조정된 결정계수 값 0.23과 0.52보다 높게 나타났으며, MAE와 RMSE 값도 3요인 모형의 값보다 낮다. Panel B의 MAPE와 RMSPE 값도 3요인 모형보다 낮다. 상태변수가 Y / C인 경우 상태변수와 시장위험의 교차 위험프리미엄(λ_SV·MKT)의 추정치가 통계적으로 유의하며, 상수항에 대한 제약조건이 없는 경우에는 상태변수와 소득증가율의 교차 위험프리미엄(λ_SV·ρc) 추정치가 통계적으로 유의하다. 조정된 결정계수, MAE, RMSE, MAPE 및 RMSPE 값도 3요인 모형보다 개선되었다. 상태변수로 SURP를 사용한 경우도 설명력이 향상되었으며, 상수항에 대한 제약조건이 있는 경우는 3요인 모형의 조정된 결정계수, MAE, RMSE, MAPE 및 RMSPE 값보다 개선되었다.

<표 10>

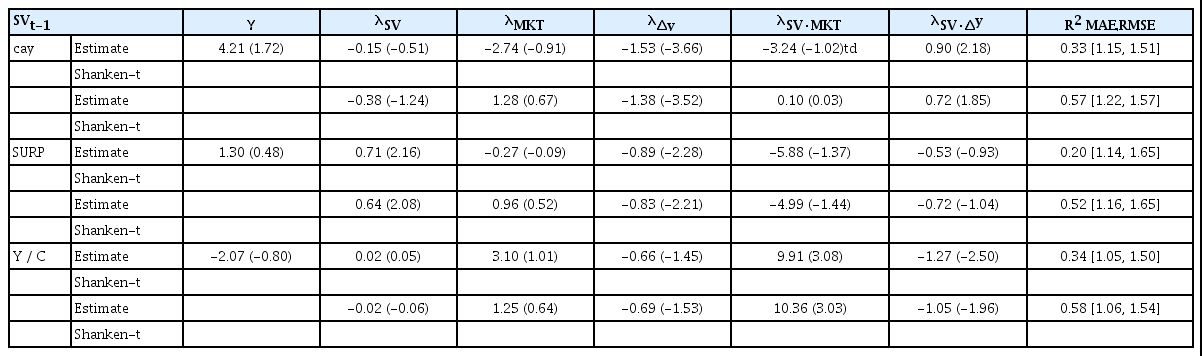
조건부 인적자본 모형 분석결과(44개 포트폴리오)

조건부 인적자본 모형의 식 Rite = λ_o + λ_SV β_SV + λ_MKT β_MKT + λ_Δy β_Δy + λ_SV·MKT β_SV·MKT + λ_SV·Δy β_SV·_Δy + v_it 을 4가지 비조건부 모형을 기업규모(size)와 장부가치 대 시장가치(book to market) 비율로 분류된 16개 포트폴리오, 주식거래 회전율(turnover) 그리고 기업 고유위험(idiosyncratic risk)으로 분류한 5분위 포트폴리오 10개 포트폴리오 및 KOSPI의 산업별 포트폴리오 18개를 사용하여 분석한 결과이다. 분석기간은 1991년 6월부터 2015년 12월까지 총 98분기이다. Panel A는 Fama and MacBeth(1973)의 방법을 이용한 횡단면 분석 결과이다. 횡단면 분석의 상수항(γ)이 0이라는 제약 여부에 따라 모형별로 2가지 위험프리미엄(λ)의 추정값과 Shanken(1992)의 표준오차에 의한 t값을 표시하였다. Jagannathan and Wang(1996)의 조정된 결정계수(adjusted R²)와 꺽쇠괄호 안에 횡단면 회귀분석의 평균절대오차(MAE)와 평균제곱근오차(RMSE)를 표시하였다. Panel B는 시계열분석의 ‘개별 포트폴리오의 상수항이 모두 0이다.’라는 귀무가설의 검정을 위한 Gibbons et al.(1989)의 GRS F값과 그 유의수준을 표시하였다. MAPE는 개별 포트폴리오별 상수항의 절대값에 대한 평균이고, RMSPE는 포트폴리오별 상수항 제곱의 평균을 다시 제곱근한 값이다.

Panel A: 위험프리미엄(λ)의 추정 결과

Panel B: 시계열분석의 상수항에 대한 분석결과

<표 11>의 조건부 소비 CAPM의 분석결과는 비조건부 모형에 비해 조정된 결정계수, MAE, RMSE, MAPE 및 RMSPE 값이 개선되었다. 상태변수로 SURP를 사용한 경우의 상태변수 위험프리미엄(λ_SV) 추정치가 상수항에 대한 제약조건이 없는 경우 유의하였다.

<표 11>

조건부 소비 CAPM 분석결과(44개 포트폴리오)

조건부 소비 CAPM 식 Rite = λ_o + λ_sv β_SV + λ_Δc β_Δc + λ_SV·Δc β_SV·Δc + v_it을 4가지 비조건부 모형을 기업규모(size)와 장부가치 대 시장가치(book to market) 비율로 분류된 16개 포트폴리오, 주식거래 회전율(turnover) 그리고 기업 고유위험(idiosyncratic risk)으로 분류한 5분위 포트폴리오 10개 포트폴리오 및 KOSPI의 산업별 포트폴리오 18개를 사용하여 분석한 결과이다. 분석기간은 1991년 6월부터 2015년 12월까지 총 98분기이다. Panel A는 Fama and MacBeth(1973)의 방법을 이용한 횡단면 분석 결과이다. 횡단면 분석의 상수항(γ)이 0이라는 제약 여부에 따라 모형별로 2가지 위험프리미엄(λ)의 추정값과 Shanken(1992)의 표준오차에 의한 t값을 표시하였다. Jagannathan and Wang(1996)의 조정된 결정계수(adjusted R²)와 꺽쇠괄호 안에 횡단면 회귀분석의 평균절대오차(MAE)와 평균제곱근오차(RMSE)를 표시하였다. Panel B는 시계열분석의 ‘개별 포트폴리오의 상수항이 모두 0이다.’라는 귀무가설의 검정을 위한 Gibbons et al.(1989)의 GRS F값과 그 유의수준을 표시하였다. MAPE는 개별 포트폴리오별 상수항의 절대값에 대한 평균이고, RMSPE는 포트폴리오별 상수항 제곱의 평균을 다시 제곱근한 값이다.

Panel A: 위험프리미엄(λ)의 추정 결과

<표 12>는 조건부 3요인 모형의 분석결과이다. 상태변수가 cay인 경우 조정된 결정계수, MAE와 RMSE가 개선되었으며, 상수항에 대한 제약조건이 있는 경우에만 상태변수의 위험프리미엄(λ_SV) 추정치가 통계적으로 유의하다. 상태변수가 SURP인 경우 상수항에 대한 제약조건이 없는 경우의 상태변수 위험프리미엄(λ_SV) 추정치가 통계적으로 유의하였고, 조정된 결정계수의 값이 가장 크게 나타났다.

<표 12>

조건부 3요인 모형 분석결과(44개 포트폴리오)

3요인 모형의 위험요인 중 MKT의 계수를 소비관련 거시변수의 선형함수로 가정한 3요인 모형의 식 Rite = λ_o + λ_SV β_SV + λ_MKT β_MKT + λ_SMB β_SMB + λ_HML β_HML + λ_SV·MKT β_SV·MKT + V_it 을 기업규모(size)와 장부가치 대 시장가치(book to market) 비율로 분류된 16개 포트폴리오와 주식거래 회전율(turnover) 그리고 기업 고유위험(idiosyncratic risk)으로 분류한 5분위 포트폴리오 10개 포트폴리오 및 KOSPI의 산업별 포트폴리오 18개를 사용하여 분석한 결과이다. 분석기간은 1991년 6월부터 2015년 12월까지 총 98분기이다. Panel A는 Fama and MacBeth(1973)의 방법을 이용한 횡단면 분석 결과이다. 횡단면 분석의 상수항(γ)이 0이라는 제약 여부에 따라 모형별로 2가지 위험프리미엄(λ)의 추정값과 Shanken (1992)의 표준오차에 의한 t값을 표시하였다. Jagannathan and Wang(1996)의 조정된 결정계수(adjusted R²)와 꺽쇠괄호 안에 횡단면 회귀분석의 평균절대오차(MAE)와 평균제곱근오차(RMSE)를 표시하였다. Panel B는 시계열분석의 ‘개별 포트폴리오의 상수항이 모두 0이다.’라는 귀무가설의 검정을 위한 Gibbons et al.(1989)의 GRS F값과 그 유의수준을 표시하였다. MAPE는 개별 포트폴리오별 상수항의 절대값에 대한 평균이고, RMSPE는 포트폴리오별 상수항 제곱의 평균을 다시 제곱근한 값이다.

Panel A: 위험프리미엄(λ)의 추정 결과

본 연구의 실증분석 결과는 다음과 같다. 첫째로, 비조건부 모형의 비교에서 소비증가율만을 위험요인으로 가지는 소비 CAPM의 설명력은 주가지수 초과수익률을 위험요인으로 포함하는 CAPM과 인적자본 모형에 비해 상대적으로 떨어지는 것으로 나타났다. 3요인 모형은 우월한 설명력을 보여주지만, 모형의 체계적 위험요인이 이론적 근거가 취약하다는 한계가 있다. 둘째, 4가지 기본모형의 실증분석은 위험프리미엄이 일정하다는 가정을 가지고 있는데, 위험 프리미엄은 시간에 따라 변화할 수 있다. 따라서 위험프리미엄에 대한 예측력을 가지고 있는 소비관련 거시변수를 시간가변적 위험프리미엄을 포착하는 상태변수로 사용한 조건부 모형의 설명력을 비조건부 모형의 설명력과 비교하였다. 상태변수를 포함한 조건부 모형은 비조건부 모형에 비해 대체로 조정된 결정계수 값이 향상되고 MAE, RMSE, MAPE 및 RMSPE 값도 개선되었는데, 시간가변적 위험프리미엄을 모형에 반영하게 되어 설명력이 향상된 것으로 해석할 수 있다. 셋째, 분석의 대상 포트폴리오로 기업규모와 장부가치 대 시장가치로 분류된 16개 포트폴리오를 사용한 경우와 강건성 분석으로 16개 포트폴리오에 거래회전율 및 기업 고유위험으로 분류된 5분위 포트폴리오 10개와 업종별 포트폴리오 18개를 추가한 44개 포트폴리오를 사용하는 경우 모두 유사한 결과가 나타났다. 마지막으로 실증분석 결과에서 시간가변적 위험프리미엄을 포착하는 상태변수로 cay를 사용하고, 시장포트폴리오의 위험자산을 확장한 인적자본 모형의 경우, 분석 대상 포트폴리오에 상관없이, Fama and French(1993)의 3요인 모형과 유사한 수준의 설명력을 가지고 있는 것으로 나타났으며, 상태변수로 Y / C를 사용한 조건부 인적자본 모형의 설명력도 16개 포트폴리오를 사용한 경우 설명력이 상대적으로 크게 향상되었으며, 강건성 분석에서는 3요인 모형과 유사한 수준의 설명력을 갖는 것으로 나타났다.

4. 결론

본 연구는 거시변수를 사용한 조건부 자산가격모형에 대한 실증분석이다. CAPM, 소득증가율을 포함하는 인적자본 모형, 소비증가율이 위험요인인 소비 CAPM 및 Fama and French(1993)의 3요인 모형을 기본모형으로 사용하였다. 시간가변적 위험프리미엄을 반영하기 위해 기본모형에 소비관련 거시변수를 상태변수로 추가한 조건부 자산가격모형의 횡단면 분석을 실시하고, 거시변수가 자산의 수익률과 유의적인 관계를 가지는지 검증하였으며 모형의 설명력을 Fama and French(1993)의 3요인 모형의 설명력과 비교하였다.

조건부 자산가격모형의 실증분석에는 위험자산의 초과수익률에 대한 예측력을 가지는 상태변수가 필요하다. 분석에 사용한 소비관련 거시변수는 Lettau and Ludvigson(2001)의 총자산 대비 소비비율, Campbell and Cochrane(1999)의 잉여소비비율의 대용치인 Wachter (2006)의 잉여소비비율, Santos and Veronesi(2006)의 소비 대비 소득비율이다. Park et al.(2019)의 연구에서 국내 종합주가지수에 대한 예측력이 검증된 세 가지 소비관련 거시변수를 조건부모형의 상태변수로 사용하였다. 모형 비교에 있어서 소표본의 검정력 문제를 해결하기 위해 기존 연구에서 제시한 여러 분석지표를 사용하고, 분석의 대상 포트폴리오로 우선 기업규모와 장부가치 대 시장가치 비율로 분류한 포트폴리오를 사용하고, 강건성 검증을 위해 거래회전율, 기업 고유위험 및 업종으로 분류된 포트폴리오를 추가하여 사용하였다.

분석 결과 기본모형 중 3요인 모형의 설명력이 높게 나타났으며, CAPM과 인적자본 모형의 설명력이 유사하고 소비 CAPM의 설명력이 상대적으로 떨어지는 것으로 나타났다. 조건부 자산가격모형은 비조건부모형에 비해 설명력이 향상되었는데, 특히 금융자산과 자영업자의 소득을 포함하여 계산한 총자산 대비 소비비율(cay)과 자영업자의 소득을 포함하여 계산한 소득을 소비로 나누어 계산한 소비 대비 소득비율(Y / C)을 상태변수로 사용한 경우 설명력이 많이 향상되었다. 기본모형 중 인적자본 모형에 상태변수로 Lettau and Ludvigson(2001)의 총자산 대비 소비비율을 추가한 조건부 인적자본 모형의 설명력은 Fama and French(1993)의 3요인 모형과 유사한 수준이었다.

CAPM은 시장 포트폴리오와 개별자산 간의 관계를 설명할 수 있으나, 1기간 모형이기 때문에 실증분석에서 시간가변적인 자산의 수익률을 설명하는데 어려움이 있을 뿐 아니라 위험자산의 수익률과 경제변수와의 관계를 규명하는데도 한계가 있다. 반면에 소비관련 거시변수를 사용한 조건부 자산가격모형은 주식 포트폴리오 간 횡단면적 수익률 차이를 거시경제변수의 변화 및 이론에 기반한 모형으로 설명하였다는데 그 의의가 있으며, 국내 주식시장의 경우에도 해외의 선행연구와 마찬가지로 소비관련 거시변수를 상태변수로 사용하는 조건부 모형의 설명력이 모방 포트폴리오에 기반한 다요인 모형에 못지않음을 보여준다.

Notes

¹⁾

소비기반 자산가격 모형에 대한 여러 주제와 자산가격 모형의 횡단면 분석에 대한 내용은 Ludvigson (2013)과 Kan and Robotti(2012)에 정리되어 있다. 소비를 활용한 국내 실증분석 중 소비 CAPM에 대한 연구사례로는 Koo(1992)와 Choi and Baek(1992)의 연구가 있으며, Dokko et al.(2001)은 소비변수를 사용하여 주식의 위험프리미엄을 실증분석하였다. 반면, 소비관련 변수를 자산수익률의 예측력 분석에 사용한 연구는 그 사례가 적으며, Kang(2013)과 Park et al.(2019)의 연구 등이 있다. 조건부 자산가격모형에 대한 실증분석 또한 그 사례가 드물다. Kook and Han(1999)은 CAPM과 인적자본 모형에 대한 조건부모형의 설명력을 실증분석하였다. 상태변수로는 금리 스프레드를 사용하였는데, 연구 당시 금리자료의 제약으로 3년 만기 회사채와 금융채의 금리 스프레드를 상태변수로 사용하였으며, 조건부모형의 설명력이 비조건부모형에 비해 향상되었음을 보였다.

²⁾

다요인 모형의 대표적인 예로 시장위험과 함께 기업규모 그리고 장부가치 대 시장가치를 체계적 위험요인의 대용치로 포함하는 3요인 및 모멘텀을 포함하는 4요인 모형이 제안되었고(Fama and French, 1993; Carhart, 1997), 이후 Fama and French(2015, 2016)에 의해 수익성(profitability)과 투자(investment)라는 2가지 위험요인을 추가한 5요인 모형이 제시되었다. 우리나라의 주식시장에 대한 위험요인 및 다요인 모형에 대한 연구로는 Yoon et al.(2009) 및 Hahn and Yoon(2016)의 연구가 있는데, 한국 주식시장의 위험요인을 다각도로 분석하고 위험요인을 모방하는 포트폴리오의 구성방법을 새롭게 제안하였다. 제시된 3요인 모형은 시장, 기업규모 및 주식 거래회전율을 위험요인으로 가지며, 실증분석에서 Fama and French(1993)의 3요인 모형보다 한국 주식 포트폴리오의 위험과 초과수익률 평가에 더 적합하다고 주장하였다.

³⁾

장부가치는 자본총액에서 우선주 자본금을 차감하여 계산하였다.

References

1. Carhart M. M. 1997;On Persistence in Mutual Fund Performance. The Journal of Finance 52(1):57–82.

2. Campbell J. Y, Cochrane J. H. 1999;By Force of Habit:A Consumption-Based Explanation of Aggregate Stock Market Behavior. Journal of political Economy 107(2):205–251.

3. Choi W, Baek Y. H. 1992;The Stock Returns and Consumption. Korean Journal of Financial Studies 14:401–424.

4. Dimson E. 1979;Risk Measurement when Shares are Subject to Infrequent Trading. Journal of Financial Economics 7(2):197–226.

5. Dokko Y, Park J. W, Cho J. H. 2001;The Equity Premium Puzzle:The Case in Korea. Asian Review of Financial Research 14(1):1–22.

6. Fama E. F, French K. R. 1993;Common Risk Factors in the Returns on Stocks and Bonds. Journal of Financial Economics 33(1):3–56.

7. Fama E. F, French K. R. 1996;Multifactor Explanations of Asset Pricing Anomalies. The Journal of Finance 51(1):55–84.

8. Fama E. F, French K. R. 2015;A Five-Factor Asset Pricing Model. Journal of Financial Economics 116:1–22.

9. Fama E. F, French K. R. 2016;Dissecting Anomalies with a Five-Factor Mode. The Review of Financial Studies 29(1):69–103.

10. Fama E. F, MacBeth J. D. 1973;Risk, Return, and Equilibrium:Empirical Tests. Journal of Political Economy 81(3):607–636.

11. Gibbons M. R, Ross S. A, Shanken J. 1989;A Test of the Efficiency of a Given Portfolio. Econometrica 5(5):1121–1152.

12. Gollin D. 2002;Getting Income Shares Right. Journal of Political Economy 110(2):458–474.

13. Hahn J, Yoon H. 2016;Determinants of the Cross-Sectional Stock Returns in Korea:Evaluating Recent Empirical Evidence. Pacific-Basin Finance Journal 38:88–106.

14. Jagannathan R, Wang Z. 1996;The Conditional CAPM and the Cross?Section of Expected Returns. The Journal of Finance 51(1):3–53.

15. Kan R, Robotti C. Handbook of Computational Finance Springer. Berlin, Heidelberg: 2012. p. 223–251.

16. Kang W. 2013;A Study on the Explanatory Power for Future Stock Returns of Changes in Consumption-Wealth Ratio:In Case of Korean Economy. Korean Journal of Financial Management 30(3):69–99.

17. Kim B. 2013;What Explains Movements in the Labor Income Share in the Korean Economy? Economic Analysis 19(3):1–48.

18. Koo B. Y. 1992;An Empirical Analysis of the Consumption-based CAPM. The Korean Journal of Financial Management 9(1):1–23.

19. Kook C. P, Han S. I. 1999;The Cross-Sectional Explanation of the Variation in Expected Stock Returns Using Conditional CAPM. Asian Review of Financial Research 12(1):147–180.

20. Lettau M, Ludvigson S. 2001a;Consumption, Aggregate wealth, and Expected Stock Returns. The Journal of Finance 56(3):815–849.

21. Lettau M, Ludvigson S. 2001b;Resurrecting the (C) CAPM:A Cross-Sectional Test when Risk Premia are Time-Varying. Journal of Political Economy 109(6):1238–1287.

22. Lewellen J, Nagel S. 2006;The Conditional CAPM does not Explain Asset-Pricing Anomalies. Journal of Financial Economics 82(2):289–314.

23. Lewellen J, Nagel S, Shanken J. 2010;A Skeptical Appraisal of Asset Pricing Tests. Journal of Financial Economics 96(2):175–194.

24. Lintner J. 1965;Security Prices, Risk, and Maximal Gains from Diversification. The Journal of Finance 20:587–615.

25. Ludvigson S. C. 2013;Advances in Consumption-Based Asset Pricing:Empirical Tests. Handbook of the Economics of Finance 2:799–906.

26. Mossin J. 1966;Equilibrium in a Capital Asset Market. Econometrica 34(4):768–783.

27. Park D, Eom Y. H, Hahn J. 2019;Forecasting Asset Returns Using Consumption-Based Measures. Journal of Money and Finance 33(1):105–149.

28. Santos T, Veronesi P. 2006;Labor Income and Predictable Stock Returns. The Review of Financial Studies 19(1):1–44.

29. Shanken J. 1992;On the Estimation of Beta-Pricing Models. The Review of Financial Studies 5(1):1–33.

30. Sharpe W. F. 1964;Capital Asset Prices:A Theory of Market Equilibrium under Conditions of Risk. The Journal of Finance 19:425–422.

31. Stock J. H, Watson M. W. 1993;A Simple Estimator of Cointegrating Vectors in Higher Order Integrated Systems. Econometrica 61(4):783–820.

32. Wachter J. A. 2006;A consumption-Based Model of the Term Structure of Interest Rates. Journal of Financial Economics 79(2):365–399.

33. Yoon S. Y, Ku B. I, Eom Y. H, Hahn J. 2009;The Cross-Section of Stock Returns in Korea:An Empirical Investigation. Asian Review of Financial Research 22(1):1–44.

Article information Continued

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

	평균 초과수익률				t(RM^e_it)

	Low	2	3	High	Low	2	3	High
Small	0.59	3.83	5.48	7.11	0.27	1.81	2.53	2.84
2	-0.22	1.71	3.86	4.96	-0.10	0.92	1.84	2.17
3	-0.25	1.78	2.86	4.25	-0.14	0.99	1.53	1.85
Big	1.50	1.31	2.12	4.70	0.87	0.79	1.07	2.02

Panel B: 분류기준 별 5분위 포트폴리오

거래회전율	Low		2	3		4	High

평균 초과수익률	2.74		0.87	1.13		0.58	-2.56

t(RM^e_it)	1.66		0.50	0.59		0.31	-1.32

기업고유위험	Low		2	3		4	High

평균 초과수익률	1.86		1.16	1.91		1.26	-2.78
t(RM^e_it)	1.10		0.72	0.95		0.65	-1.40

Panel C: 산업별 포트폴리오

	평균 초과수익률		t(RM^e_it)			평균 초과수익률	t(RM^e_it)

음식료품	2.06		1.24	운수장비		0.93	0.47
섬유, 의복	-0.40		-0.22	유통업		0.04	0.02
종이, 목재	-0.74		-0.41	건설업		-0.52	-0.21
화학	2.11		1.12	운수창고		1.50	0.63
의약품	2.63		1.37	금융업		-0.48	-0.21
비금속광물	1.18		0.53	은행		-0.80	-0.35
철강및금속	1.81		0.91	증권		2.33	0.57
기계	-0.18		-0.09	보험		3.38	1.42
전기, 전자	2.46		1.16	제조업		1.45	0.84

	MKT	SMB	HML	Δy	Δc	cay	SURP	Y / C
Panel A: 기초통계량
평균	1.07	0.12	4.39	0.46	0.66	-0.06	0.009	1.30
표준편차	16.41	16.34	11.44	1.98	1.41	0.05	0.004	0.12

Panel B: 상관계수

	MKT	SMB	HML	Δy	Δc	cay	SURP	Y / C

MKT	1	-0.18 ^*	0.37 ^***	0.06	-0.04	-0.01	-0.13	-0.10
SMB		1	-0.06	0.08	0.09	-0.20 ^*	0.04	0.12
HML			1	-0.06	-0.10	0.07	0.03	0.00
Δy				1	0.57 ^***	-0.02	-0.02	-0.05
Δc					1	-0.20 ^*	0.17 ^*	0.20 ^**
cay						1	0.04	-0.44 ^***
SURP							1	0.82 ^***
Y / C								1

		γ	λ_MKT	λ_Δy	λ_Δc	λ_SMB	λ_HML	R²MAE, RMSE
CAPM	Estimate	-4.74 (-1.31)	8.13 (2.15)					0.28 [1.35, 1.69]
	Shanken-t
	Estimate		3.17 (1.66)					0.71 [1.58, 1.84]
	Shanken-t
인적자본모형	Estimate	-4.90 (-1.36)	8.35 (2.22)	0.24 (0.47)				0.23 [1.35, 1.69]
	Shanken-t
	Estimate		3.12 (1.60)	-0.17 (-0.31)				0.69 [1.58, 1.84]
	Shanken-t
소비 CAPM	Estimate	3.31 (1.79)			0.34 (1.32)			-0.03 [1.74, 2.03]
	Shanken-t
	Estimate				-1.10 (-1.39)			0.26 [2.32, 2.92]
	Shanken-t
3요인 모형	Estimate	-8.74 (-2.07)	10.31 (2.26)			1.82 (0.98)	3.95 (2.96)	0.67 [0.86, 1.06]
	Shanken-t
	Estimate		1.25 (0.69)			1.56 (0.86)	4.20 (3.26)	0.86 [0.99, 1.17]
	Shanken-t

Panel B: 시계열분석의 상수항에 대한 분석결과

	CAPM		인적자본 모형		소비 CAPM		3요인 모형

GRS F test	3.84		3.73		3.69		2.11
p-value	0.00		0.00		0.00		0.02
MAPE	1.58		1.58		2.32		0.99
RMSPE	1.84		1.84		2.92		1.17

SV_t-1		γ	λ_SV	λ_MKT	λ_SV·MKT	R²MAE,RMSE
cay	Estimate	-5.78 (-1.14)	-0.60 (-2.00)	9.16 (1.73)	-7.09 (-1.66)	0.54 [1.04, 1.26]
	Shanken-t
	Estimate		-0.31 (-0.95)	3.50 (1.74)	-12.18 (-3.10)	0.83 [1.06, 1.29]
	Shanken-t
SURP	Estimate	-1.91 (-0.40)	0.16 (0.34)	4.75 (0.96)	-7.31 (-1.43)	0.30 [1.23, 1.55]
	Shanken-t
	Estimate		0.31 (0.75)	2.67 (1.35)	-8.93 (-2.69)	0.76 [1.25, 1.57]
	Shanken-t
Y / C	Estimate	-4.51 (-1.20)	0.13 (0.26)	7.90 (1.96)	12.27 (3.21)	0.51 [1.06, 1.29]
	Shanken-t
	Estimate		-0.07 (-0.12)	3.32 (1.66)	13.88 (3.45)	0.79 [1.26, 1.46]
	Shanken-t

Panel B: 시계열분석의 상수항에 대한 분석결과

		cay		SURP	Y/C

GRS F test		2.84		2.23	1.75
p-value		0.00		0.01	0.05
MAPE		1.06		1.25	1.26
RMSPE		1.29		1.57	1.46

SV_t-1		γ	λ_SV	λ_MKT	λ_Δy	λ _SV _· _MKT	λ _SV_·_Δy	R² MAE,RMSE
cay	Estimate	3.06 (0.45)	-0.52 (-1.80)	-0.79 (-0.11)	-1.06 (-1.49)	-5.47 (-1.27)	1.58 (1.69)	0.68 [0.82, 0.95]
	Shanken-t
	Estimate		-0.65 (-1.69)	2.32 (1.20)	-0.95 (-1.52)	-3.53 (-0.70)	1.37 (2.02)	0.89 [0.82, 0.96]
	Shanken-t
SURP	Estimate	8.41 (1.28)	0.25 (0.49)	-5.09 (-0.77)	-1.04 (-1.64)	-16.76 (-2.59)	1.50 (1.65)	0.36 [1.22, 1.35]
	Shanken-t
	Estimate		0.02 (0.05)	3.17 (1.71)	-0.33 (-0.57)	-9.28 (-2.66)	0.47 (0.62)	0.75 [1.23, 1.45]
	Shanken-t
Y/C	Estimate	-6.75 (-1.81)	-0.58 (-1.50)	8.90 (2.15)	0.70 (1.22)	24.46 (3.70)	-1.55 (-1.66)	0.58 [0.89, 1.09]
	Shanken-t
	Estimate		-0.40 (-1.12)	2.63 (1.39)	0.06 (0.09)	19.70 (2.81)	-0.76 (-0.78)	0.77 [1.24, 1.41]
	Shanken-t

Panel B: 시계열분석의 상수항에 대한 분석결과

			cay		SURP		Y/C

GRS F test			0.63		1.96		0.77
p-value			0.85		0.03		0.72
MAPE			0.82		1.23		1.24
RMSPE			0.96		1.45		1.41

SV_t-1		γ	λ_SV	λ_ΔC	λ_SV·ΔC	R² MAE, RMSEm
cay	Estimate	2.72 (1.46)	-0.34 (-1.08)	0.55 (1.98)	1.36 (2.67)	0.29 [1.27, 1.56]
	Shanken-t
	Estimate		-0.72 (-1.88)	-0.47 (-0.71)	0.94 (2.17)	0.56 [1.85, 2.11]
	Shanken-t
SURP	Estimate	-0.74 (-0.26)	0.35 (0.77)	0.71 (1.83)	-0.57 (-1.01)	-0.04 [1.59, 1.88]
	Shanken-t
	Estimate		0.42 (0.84)	0.69 (1.89)	-0.37 (-0.74)	0.65 [1.60, 1.89]
	Shanken-t
Y / C	Estimate	-7.19 (-2.65)	-1.10 (-2.62)	1.31 (3.21)	-2.80 (-3.91)	0.30 [1.27, 1.54]
	Shanken-t
	Estimate		-0.07 (-0.15)	0.78 (2.37)	-0.56 (-0.93)	0.69 [1.43, 1.76]
	Shanken-t

Panel B: 시계열분석의 상수항에 대한 분석결과

	cay			SURP	Y / C
GRS F test	1.05			1.06	1.00
p-value	0.42			0.41	0.47
MAPE	1.85			1.60	1.43
RMSPE	2.11			1.89	1.76

SV_t-1		γ	λ_SV	λ_MKT	λ_SMB	λ_HML	λ_SV·MKT	R ² MAE,RMSE
cay	Estimate	-0.34 (-0.06)	-0.34 (-1.18)	2.20 (0.37)	1.79 (0.95)	4.24 (3.12)	-7.88 (-1.80)	0.76 [0.61, 0.83]
	Shanken-t
	Estimate		-0.34 (-1.13)	1.86 (1.00)	1.78 (0.95)	4.25 (3.19)	-8.05 (-2.36)	0.92 [0.61, 0.83]
	Shanken-t
SURP	Estimate	-11.75 (-2.65)	-0.70 (-1.69)	13.27 (2.73)	1.77 (0.91)	4.15 (2.95)	4.24 (1.07)	0.66 [0.76, 0.99]
	Shanken-t
	Estimate		-0.25 (-0.63)	1.21 (0.67)	1.55 (0.85)	4.09 (3.07)	-1.31 (-0.39)	0.84 [0.95, 1.15]
	Shanken-t
Y / C	Estimate	-6.34 (-1.29)	-0.70 (-1.59)	8.27 (1.55)	1.65 (0.83)	4.96 (3.37)	12.82 (3.21)	0.78 [0.62, 0.80]
	Shanken-t
	Estimate		-0.49 (-1.24)	1.81 (0.94)	1.48 (0.76)	5.23 (3.74)	13.22 (3.44)	0.91 [0.68, 0.86]
	Shanken-t

Panel B: 시계열분석의 상수항에 대한 분석결과

			cay		SURP		Y / C

GRS F test			0.91		1.89		0.53
p-value			0.56		0.03		0.92
MAPE			0.61		0.95		0.68
RMSPE			0.83		1.15		0.86

		γ	λMKT	λ_Δy	λ_Δc	λ_SMB	λ_HML	R² MAE,RMSE
CAPM	Estimate	0.22 (0.09)	1.40 (0.50)					0.00 [1.46, 1.94]
	Shanken-t
	Estimate		1.61 (0.92)					0.40 [1.46, 1.94]
	Shanken-t
인적자본모형	Estimate	-0.46 (-0.18)	1.95 (0.68)	-1.00 (-2.62)				0.11 [1.26, 1.81]
	Shanken-t
	Estimate		1.50 (0.83)	-0.98 (-2.31)				0.46 [1.24, 1.81]
	Shanken-t
소비 CAPM	Estimate	1.57 (0.84)			-0.02 (-0.07)			-0.02 [1.46, 1.96]
	Shanken-t
	Estimate				-0.68 (-0.95)			0.19 [1.65, 2.25]
	Shanken-t
3요인 모형	Estimate	2.47 (0.92)	-1.73 (-0.56)			1.07 (0.59)	3.08 (2.29)	0.23 [1.27, 1.67]
	Shanken-t
	Estimate		0.67 (0.39)			1.40 (0.77)	2.84 (2.05)	0.52 [1.36, 1.70]
	Shanken-t

	CAPM	인적자본 모형	소비 CAPM	3요인 모형
GRS F test	4.36	3.21	3.16	5.13
p-value	0.00	0.00	0.00	0.00
MAPE	1.46	1.24	1.65	1.36
RMSPE	1.94	1.81	2.25	1.70

SV_t-1		γ	λ_SV	λ_MKT	λ_SV · _MKT	R² MAE,RMSE
cay	Estimate	2.05 (0.97)	-0.27 (-1.07)	-0.28 (-0.10)	-3.62 (-1.24)	0.07 [1.41, 1.82]
	Shanken-t
	Estimate		-0.38 (-1.42)	1.67 (0.94)	-1.95 (-0.62)	0.44 [1.42, 1.83]
	Shanken-t
SURP	Estimate	2.56 (0.83)	1.07 (3.20)	-1.06 (-0.33)	-4.30 (-1.07)	0.10 [1.28, 1.79]
	Shanken-t
	Estimate		0.85 (2.66)	1.54 (0.83)	-1.39 (-0.41)	0.44 [1.30, 1.83]
	Shanken-t
Y / C	Estimate	0.76 (0.32)	0.40 (1.28)	0.94 (0.34)	4.16 (1.38)	0.10 [1.34, 1.79]
	Shanken-t
	Estimate		0.44 (1.18)	1.66 (0.92)	3.51 (0.83)	0.46 [1.34, 1.80]
	Shanken-t

	cay	SURP	Y / C
GRS F test	3.97	2.42	3.36
p-value	0.00	0.00	0.00
MAPE	1.42	1.30	1.34
RMSPE	1.83	1.83	1.80

SV_t-1		γ	λ_SV	λ_MKT	λ_Δy	λ_SV·MKT	λ_SV·Δy	R² MAE,RMSE
cay	Estimate	4.21 (1.72)	-0.15 (-0.51)	-2.74 (-0.91)	-1.53 (-3.66)	-3.24 (-1.02)td	0.90 (2.18)	0.33 [1.15, 1.51]
	Shanken-t
	Estimate		-0.38 (-1.24)	1.28 (0.67)	-1.38 (-3.52)	0.10 (0.03)	0.72 (1.85)	0.57 [1.22, 1.57]
	Shanken-t
SURP	Estimate	1.30 (0.48)	0.71 (2.16)	-0.27 (-0.09)	-0.89 (-2.28)	-5.88 (-1.37)	-0.53 (-0.93)	0.20 [1.14, 1.65]
	Shanken-t
	Estimate		0.64 (2.08)	0.96 (0.52)	-0.83 (-2.21)	-4.99 (-1.44)	-0.72 (-1.04)	0.52 [1.16, 1.65]
	Shanken-t
Y / C	Estimate	-2.07 (-0.80)	0.02 (0.05)	3.10 (1.01)	-0.66 (-1.45)	9.91 (3.08)	-1.27 (-2.50)	0.34 [1.05, 1.50]
	Shanken-t
	Estimate		-0.02 (-0.06)	1.25 (0.64)	-0.69 (-1.53)	10.36 (3.03)	-1.05 (-1.96)	0.58 [1.06, 1.54]
	Shanken-t

	cay	SURP	Y / C
GRS F test	2.18	2.27	1.76
p-value	0.00	0.00	0.03
MAPE	1.22	1.16	1.06
RMSPE	1.57	1.65	1.54

SV_t-1		γ	λ_SV	λ_ΔC	λ_{SV · ΔC}	R² MAE,RMSE
cay	Estimate	1.40 (0.74)	-0.40 (-1.83)	-0.02 (-0.07)	-0.18 (-0.73)	0.04 [1.35, 1.85]
	Shanken-t
	Estimate		-0.43 (-1.90)	-0.57 (-0.84)	-0.24 (-1.01)	0.27 [1.60, 2.08]
	Shanken-t
SURP	Estimate	1.46 (0.82)	0.68 (2.12)	0.38 (1.23)	0.18 (0.48)	0.10 [1.37, 1.80]
	Shanken-t
	Estimate		0.37 (0.75)	0.25 (0.79)	-0.31 (-0.49)	0.44 [1.38, 1.83]
	Shanken-t
Y / C	Estimate	-0.28 (-0.15)	0.49 (1.51)	0.44 (1.30)	-0.15 (-0.40)	0.15 [1.29, 1.74]
	Shanken-t
	Estimate		0.51 (1.50)	0.44 (1.37)	-0.07 (-0.12)	0.49 [1.28, 1.74]
	Shanken-t

Panel B: 시계열분석의 상수항에 대한 분석결과

		cay		SURP		Y / C

GRS F test		2.80		2.09		1.94
p-value		0.00		0.01		0.01
MAPE		1.60		1.38		1.28
RMSPE		2.08		1.83		1.74

SV_t-1		γ	λ_SV	λ_MKT	λ_SMB	λ_HML	λ_SV ·_MKT	R² MAE,RMSE
cay	Estimate	2.92 (1.29)	-0.41 (-1.90)	-1.88 (-0.66)	1.20 (0.64)	2.83 (2.08)	-1.08 (-0.34)	0.26 [1.21, 1.59]
	Shanken-t
	Estimate		-0.52 (-2.35)	0.86 (0.48)	1.42 (0.77)	2.81 (2.07)	0.97 (0.28)	0.54 [1.27, 1.61]
	Shanken-t
SURP	Estimate	1.35 (0.56)	0.69 (2.06)	-0.71 (-0.24)	1.47 (0.76)	4.01 (2.83)	2.01 (0.58)	0.32 [1.15, 1.52]
	Shanken-t
	Estimate		0.60 (1.79)	0.57 (0.31)	1.56 (0.81)	4.09 (2.88)	3.38 (0.88)	0.59 [1.17, 1.53]
	Shanken-t
Y / C	Estimate	3.62 (1.38)	0.42 (1.48)	-2.54 (-0.82)	1.06 (0.56)	3.39 (2.39)	3.24 (1.02)	0.28 [1.21, 1.57]
	Shanken-t
	Estimate		0.37 (1.41)	0.89 (0.51)	1.49 (0.82)	2.97 (2.05)	2.03 (0.58)	0.53 [1.31, 1.64]
	Shanken-t

Panel B: 시계열분석의 상수항에 대한 분석결과

		cay			SURP		Y / C

GRS F test		4.37			2.95		4.38
p-value		0.00			0.00		0.00
MAPE		1.27			1.17		1.31
RMSPE		1.61			1.53		1.64