레버리지 ETF의 추적오차 관점에서 운용상 제도적 제약
Institutional Constraints on the Rate of Derivatives in Leveraged Exchange-Traded Fund
Article information
Abstract
본 연구에서는 파생상품의 위험평가액을 ETF(Exchange-Traded Fund)의 순자산으로 나눈 ‘파생상품 비율’ 제한이 레버리지 ETF 추적오차에 미치는 영향을 분석했다. 그 결과, 세 가지 결론을 도출하였다. 첫째, 파생상품 비율이 100%로 제한되고 있을 당시에 지수를 2배 추종하는 레버리지 ETF의 추적오차는 파생상품 비율의 영향을 받는다. 둘째, 파생상품 비율이 200%로 완화하여 제한된 이후에 출시한 선물지수를 2배 추종하는 레버리지 ETF의 당일 추적오차는 파생상품 비율의 영향을 받는다. 셋째, 파생상품 비율의 제한과 관련하여, 선물지수를 2배 추종하는 레버리지 ETF 자료에서 파생상품 비율이 200%에 가까운 자료와 그렇지 않은 자료를 구분하여 분석하였다. 그 결과, 파생상품 비율의 200% 제한을 약간 초과하더라도 제한비율에 가까운 자료가 그렇지 않은 자료보다 더 낮은 추적오차를 가지고 있었다. 이것은 파생상품 비율을 제도적으로 제한 할 경우, 선물지수를 2배 추종하는 레버리지 ETF의 운용에 제약이 될 수 있음을 시사한다.
Trans Abstract
This study confirmed whether the rate of derivatives in leveraged exchange-traded funds (ETF) calculated by derivatives and net asset value (NAV) affect their tracking errors. This research established three findings. First, when the rate of derivatives was limited at 100%, the tracking error of the leveraged ETF targeted on 2 times of the index was affected by the rate of derivatives. Second, when the rate of derivatives was eased to 200%, the same-day tracking error of the leveraged ETF targeted on 2 times of the futures index that launched after the constraints was affected by the rate of derivatives. Third, this study analyzed the constraints of the rate of derivatives after determining whether the leveraged ETF targeted on 2 times of the index indicates whether the rate of derivatives is close to 200%. As a result, even when the rate of derivatives is slightly over the 200% limit, the tracking error was lower. Even when the constraints were slightly over the limit, the tracking error was shown to be significantly lower than the other data set. This result implies that when there is an institutional constraint on the rate of derivatives, there can be limitations to fund management of leveraged ETF targeted on 2 times of the futures index.
1. 서론
상장지수펀드라는 의미를 가지고 있는 ETF(Exchange-Traded Fund)는 Kang(2013), Kim and Choi(2018)에 언급된 바와 같이 주가지수에 연계되어 수익이 결정되는 펀드를 말한다. 이러한 ETF들은 Lee and Hong(2004), Choi and Lee(2012), Kim and Park(2017)의 연구에서 언급된 것처럼 기존의 펀드들과 다르게 시장에서 직접 거래할 수 있는 장점을 가지고 있다. 그리고 Kang et al.(2014), Choi and Yi(2016)에서 언급된 것과 같이 ETF는 1989년 북미에서 처음 상장되어 거래되기 시작했고, 국내의 경우는 <그림 1>과 같이 2002년에 시가총액 기준으로 약 3,854억 원 규모로 시작하여, 현재 약 40조 원의 규모로 크게 성장하였다.
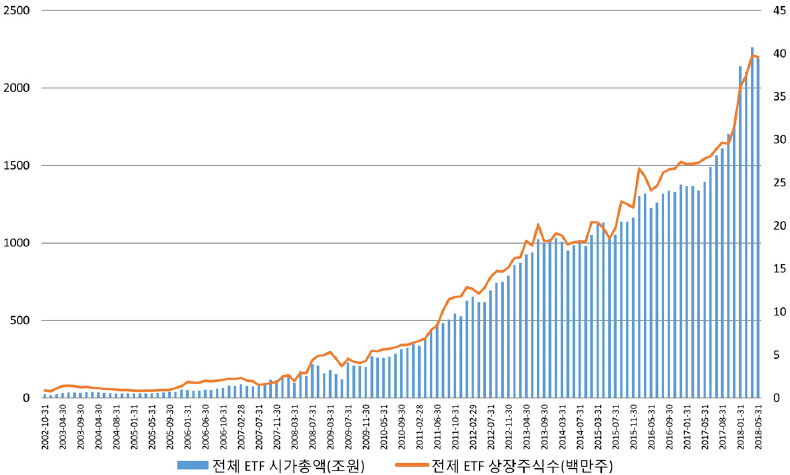
기간별 ETF 상장주식수와 시가총액
가로축은 2002년 1월부터 2018년 5월까지 기간을 의미하고, 왼쪽 세로축은 각 기간의 ETF 상장증권수를 의미해 주황색 실선으로 표시하였고, 오른쪽 세로축은 거래되는 ETF들의 시가총액을 파란색 막대그래프로 표시하였다.
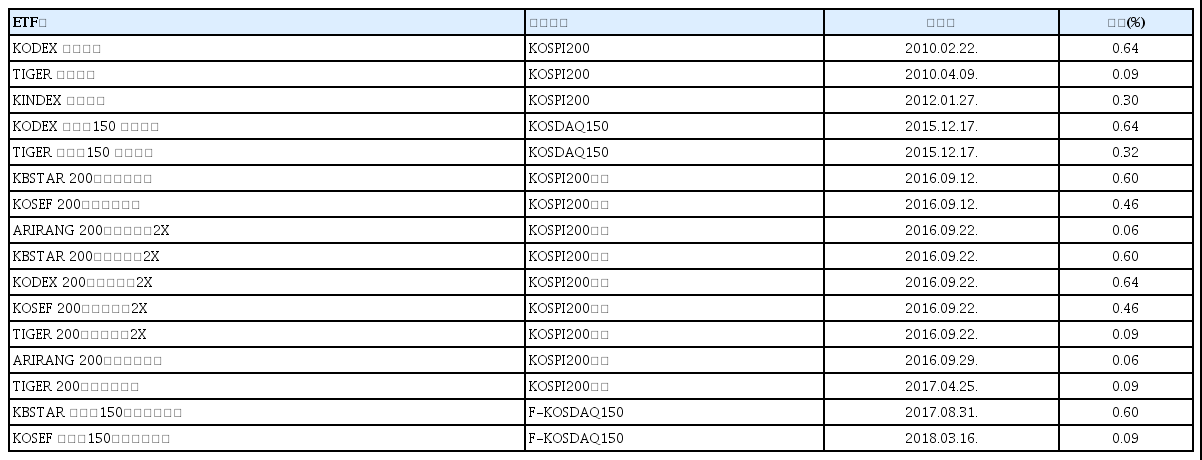
이렇게 성장한 ETF는 시가총액을 기준으로 규모의 측면만 아니라 다양성 측면에서도 많은 발전이 있었는데, 그 중에 대표적인 상품이 레버리지 관련 ETF이다. 레버리지 ETF는 Lee(2013), Kim(2016)에서와 같이 추종하는 지수와 비교해 2배로 성과가 나타나도록 설계된 펀드를 의미 한다.1), 예를 들어 KOSPI200 지수를 그대로 추종하는 ETF의 경우, 당일 지수가 1% 상승하거나 하락하면 해당 ETF는 동일하게 1% 상승하거나 하락하도록 설계되었지만, 레버리지 ETF의 경우, 그 2배인 2% 상승 혹은 하락이 발생하도록 설계되어 있다.2), 이러한 레버리지 ETF의 경우, <표 1>과 같이 2010년 2월 KOSPI200 지수를 2배 추종하는 KODEX 레버리지가 출시되었고, 이후에 TIGER 레버리지, KINDEX 레버리지가 출시되어 거래되다가, 그 이후에 KODAQ150 지수가 발표됨에 따라 2015년 12월에 이것을 2배로 추종하는 KODEX 코스닥150 레버리지, TIGER 코스닥 150 레버리지도 출시되어 점차 지수를 2배 추종하는 레버리지 ETF의 상장종목수가 증가하였다.
이러한 지수를 2배 추종하는 레버리지 ETF의 운용상 특징은 KOSPI200이나 KODAQ150과 같이 해당 지수를 2배로 추종함에 있어서, 해당 지수에 속해있는 주식들을 포트폴리오로 구성하고, 2배의 레버리지를 맞추기 위해 추가로 해당 지수의 선물계약을 이용하여, 그 목표를 달성하고 있다는 것이다. 하지만 2016년 6월까지만 하더라도 이러한 레버리지 ETF 운용에 있어서 자본시장법 제 81조 ① 1. 마 및 자본시장법 시행령 제 80조 ⑥에 의해 파생상품 위험평가액이 자산에서 부채를 뺀 순자산의 100% 이내로 제한이 있었는데, 이로 인해 펀드운용의 자율성이 낮을 수 있었다.3), 하지만 금융위원회에서는 이러한 제도적 제약과 관련하여 자본시장법 시행령 제 80조 ⑥을 개선하여 일정요건을 충족하는 ETF들에 한해 파생상품 위험평가액 한도를 100%에서 200%로 상향조정하여 완화했다. 그런데 이러한 파생상품 위혐평가액 한도조정은 기존의 지수를 2배 추종하는 레버리지 ETF의 운용에 자율성을 높이게 한 부분도 있었지만, 다른 한편으로는 <표 1>에서와 같이 KOSPI200의 선물지수를 2배 추종하거나, KOSDAQ150의 선물지수를 2배 추종하는 레버리지 ETF가 출시되는 결과를 발생시켰다.
문제는 기존의 지수를 2배 추종하는 레버리지 ETF의 경우, 추종하는 지수에 속한 주식들을 포트폴리오로 구성하고, 2배의 레버리지는 선물계약을 이용해 맞추고 있었는데, 여기서 선물 계약이 포트폴리오 구성에 주요한 역할을 한다고 볼 수는 없으나, 선물지수를 2배 추종하는 레버리지 ETF의 경우, 선물계약이 포트폴리오 구성에 있어 주요한 역할을 하게 될 수 있다는 것이다. 예를 들어, 지수를 2배 추종하는 레버리지 ETF에서는 선물지수가 아닌 지수를 2배 추종하는 목적을 가지고 있기 때문에 2배의 레버리지를 만들기 위해서 선물계약을 이용하기도 하지만 기본적으로 해당 지수를 구성하고 있는 주식 종목들을 ETF의 포트폴리오로 구성하고 선물계약은 레버리지를 위해 이용하고 있는 것에 반해 선물지수를 2배 추종하는 레버리지 ETF의 경우 지수가 아닌 선물지수 그 자체를 2배로 추종하는 목적을 가지고 있기 때문에 해당 지수를 구성하는 주식 종목들보다는 선물계약을 통해 ETF의 포트폴리오를 구성하게 되는데 이때 선물지수를 2배 추종하는 레버리지 ETF의 경우 지수를 2배 추종하는 레버리지 ETF보다 선물계약의 사용정도가 더 높을 수 있으며 결과적으로 선물계약이 주요한 역할을 할 수 있다는 것이다. 그래서 이렇게 파생상품 위험평가액 한도가 ETF의 순자산에 200%로 제한되는 제도적 상황은 결과적으로 선물지수를 2배 추종하는 레버리지 ETF 운용에 영향을 미칠 수 있다는 것이다. 즉, 지수 혹은 선물지수를 2배를 추종하는 레버리지 ETF의 운용목적은 ETF가 해당지수의 변화에 동일한 2배만큼의 상승과 하락이 이루어지도록 하는 것인데, 이러한 목적 달성은 추종지수와 비교해 추적오차를 최소화하는 것으로 볼 수 있으며, 이때 파생상품 사용제한이 운용목표에 해당되는 추적오차 감소에 영향을 미칠 수 있다는 것이다. 특히, 선물지수를 2배 추종하는 레버리지 ETF의 경우, 지수를 2배 추종하는 레버리지 ETF와 비교해 주로 선물계약을 통해 포트폴리오를 구성하여 추종지수의 2배 레버리지를 맞추는 상황인데, 현재의 파생상품 사용제한은 지수를 2배 추종하는 레버리지 ETF보다 선물지수를 2배 추종하는 레버리지 ETF의 추적오차에 영향을 줄 가능성이 더 높다는 것이다. 하지만 이러한 문제와 관련하여 현재 연구가 활발하지 않은 상황이며, 국내에서 레버리지 ETF와 관련된 연구 자체가 다른 ETF 연구들과 비교해 많지 않은 상황이다.4) 따라서 본 연구에서는 레버리지 ETF를 운용하는데 있어서 파생상품 사용을 제한하는 것이 레버리지 ETF 추적오차에 어떠한 영향을 미치는지 확인하고자 하며, 이를 통해 제도와 관련된 시사점을 제시하고자 한다.
본 연구의 결과를 간략히 요약하면 다음과 같다. 첫째, 파생상품 위험평가액을 ETF의 순자산 으로 나눈 파생상품 비율이 100%로 제한된 상황에서 지수를 2배 추종하는 레버리지 ETF의 추적오차는 파생상품 비율의 영향을 받는다. 그리고 파생상품 비율이 100%에서 200%로 완화한 이후에는 파생상품 비율이 지수를 2배 추종하고 있는 레버리지 ETF 추적오차에 영향을 미치지 않는다. 둘째, 파생상품 비율이 100%에서 200%로 완화하여 제한된 이후에 출시한 선물지수를 2배 추종하는 레버리지 ETF의 당일 추적오차는 파생상품 비율의 영향을 받는다. 셋째, 파생상품 비율이 200%로 제한되는 경우, 선물지수를 2배 추종하는 레버리지 ETF의 추적오차는 파생상품 비율제한의 영향을 받는다. 이것은 파생상품 비율을 200%로 제한하는 것이 선물지수를 2배 추종하는 레버리지 ETF의 운용에 제약이 될 수 있음을 시사한다.
본 연구는 다음과 같이 구성되어 있다. 제 2장에서는 ETF와 관련된 기존의 문헌들을 살펴 볼 것이며 제 3장에서는 본 연구를 위한 연구가설을 제시하고 분석에 필요한 자료를 소개 할 것이다. 그리고 제 4장에서는 제 3장에서 제시한 연구가설을 실증하고 해석할 것이며, 이와 관련하여 필요한 추가가설을 제시하고 분석 할 것이다. 마지막으로 제 5장에서는 지금까지 다루었던 내용을 정리하고 시사점을 제시할 것이다.
2. 문헌연구
ETF와 관련하여 현재까지 진행된 연구는 크게 시장효율성이나 추적오차, 변동성, 헷지 그리고 제도 등과 관련된 연구들이 존재하는데, 레버리지 ETF와 관련된 연구도 이러한 범주에 속하지만, 연구 자체는 다른 ETF와 비교해 활발하지는 않은 상황이다. 우선, 레버리지에 상관없이 ETF와 관련된 연구를 살펴보면, 시장효율성과 관련된 연구로 선도지연이나 가격발견, 정보전달 및 효과 등과 관련된 연구가 존재한다. 여기서 ETF 시장에서의 선도지연은 ETF가 추종지수를 따라가는 현상이 나타나는지 아니면 반대로 추종지수가 ETF를 따라가는 현상이 나타나는지 등을 확인하는 연구이고 Choi(2007), Hahn(2007), Hahn and Lee(2007)의 연구가 존재하고 있다. 또한, 가격발견, 정보전달 및 효과와 관련해서는 Kang(2009), Hahn and Han(2009), Kang et al.(2015), Yeom and Baek(2015)의 연구가 존재하며, 국외 연구로는 Chen and Chung(2012), Chu et al.(1999), So and Tae(2004), 레버리지 ETF와 관련해서는 Kim(2016)의 연구가 존재한다. 이런 연구는 여러 금융시장에서 관련된 자산이 거래되고 있을 때 하나의 새로운 정보가 발생하면, 그 정보가 여러 금융시장에 반응하는 속도와 관련된 연구이다. 결국, 이러한 ETF 관련 연구들은 ETF 상품들이 금융시장에 다른 상품들과 비교해서 시장에 효율적인지 여부를 중점적으로 연구한 것으로 ETF를 운용목적에 맞게 잘 운용했는지 여부와 ETF를 운용하는데 있어 운용상 제도적 제약을 확인하는 연구와는 차이가 있다.5)
여기서 ETF를 운용목적에 맞게 잘 운용했는지 여부를 확인하려면, 추종지수가 있는 ETF를 대상으로 해당 ETF가 추종지수를 잘 따라가는 것 이외에도, 정확하게 따라가는지 여부를 확인해야 하는데, 그러한 측정지표가 추적오차이다. 추적오차는 Hur et al.(2012)의 연구에 따르면 추종지수의 변화와 ETF의 변화의 절대적 차이를 의미하는데, 결국에는 이러한 추적오차를 최소화 하는 것이 추종지수가 있는 ETF를 잘 운용한 것이라고 볼 수 있다.6), 그래서 추적오차와 관련된 연구를 자세히 살펴보면, 앞서 언급한 Hur et al.(2012)의 경우, 추적오차의 원인을 ETF의 분배금, 추종지수의 변동성, 구성종목의 변경빈도에 따라 영향을 받지만 운용사의 운용능력은 영향이 없다고 주장을 했다. 그리고 Chung(2012)의 연구에서는 추적오차를 ETF와 추종지수의 추적오차로 정의하고, 이것을 ETF와 순자산가치인 NAV(Net Asset Value)의 추적오차, NAV와 추종지수의 추적오차로 구분하였고, ETF와 NAV의 추적오차가 많은 비중을 가지고 있다는 것을 주장했다.7), 또한, ETF가 출시되기 이전부터 존재했던 인덱스펀드와 관련하여 Choi and Lee(2012)의 경우, 인덱스펀드가 ETF 상장 이후에 추종지수를 더 강하게 추종하고 있음을 주장했다.
지수를 그대로 추종하는 ETF가 아닌 2배로 추종하는 레버리지 ETF의 추적오차와 관련해서는 Lee(2013)와 Cho(2013)의 연구가 존재한다. 먼저, Lee(2013)의 경우, 레버리지 ETF 시장가격의 수익률과 NAV의 수익률을 추종지수의 수익률과 비교해 추적오차를 산출하고 분석한 결과, 두 추적오차는 음(-)의 값을 가진다고 주장했는데, 이것은 초과성과의 개념으로서 ETF 시장가격의 수익률이 NAV의 수익률과 비교해 낮은 값을 가진다고 해석할 수 있다. 그리고 Cho(2013)의 경우, ETF 시장가격과 이를 추종하는 지수의 움직임이 동일해야 하지만 실제로는 추적오차로 인해 완전하지 못하며, 이로서 괴리율이 발생 할 수 있다고 언급했다. 그리고 괴리율을 ETF의 가격과 순자산가치의 차이를 분자로 제시하고 순자산가치를 분모로 제시한 비율로 정의해서 분석했는데, 순자산총액이 괴리율에 대해 음(-)의 영향이 있는 것으로 나타났으며, 개인투자자의 거래대금 비율이 괴리율에 양(+)의 영향을 미치는 것으로 나타난다고 주장했다.
추적오차와 관련된 외국 문헌들을 살펴보면 Gastineau(2004), Gallagher and Segara(2005)의 경우, ETF 시장에서 순자산가치인 NAV와 추종지수를 이용해 추적오차가 얼마나 나타나는지 분석하였는데, 이 연구들은 그 원인을 구체적으로 실증해보이지는 않았다. Lin and Chou(2006)의 경우, TTT라는 대만의 최초 ETF 상품에서 수수료율, 추종지수 구성종목 변경, 분배금이 추적오차에 영향을 미친다고 주장하였고, Shin and Soydemir(2010)의 연구에서는 미국 ETF 상품에서 환율변화가 추적오차에 영향을 미친다고 분석하였다. 그리고 ETF는 아니지만 지수를 추종하는 인덱스펀드와 관련하여 Frino and Gallagher(2001)는 추종지수의 위험, 구성종목 변경, 분배금 등이 추적오차를 발생시키는 원인이라고 주장했다. 그리고 성과측면에서 Elton el al.(2002)는 SPDR이라고 불리는 S&P 500 지수를 추종하는 ETF를 이용해 SPDR이 추종지수 대비 저평가 되어있음을 발견했는데, 그 원인은 분배금과 관련하여 보유계정이 분리되어 있는 제도적인 부분으로 인한 원인이라고 주장했으며, ETF와 순자산가치인 NAV의 괴리율 혹은 가격오차율 측면에서는 Ackert and Tian(2008), Kim(2018)의 문헌이 존재한다. 결국, 지금까지 언급된 추적오차와 관련된 연구들의 경우, 법적인 제도와 관련해 운용제약에 따른 추적오차의 영향을 확인하는 본 연구와 차이가 있다.
제도와 관련된 연구를 살펴보면, Lee and Moon(2009)과 같이 ETF의 과세제도와 관련된 연구나 소비자보호와 관련한 Yun(2016)의 연구, 법적규제와 관련한 Lee(2012)의 연구가 존재하는데 ETF 제도와 관련된 연구자체도 많지 않은 상황이다.8)
지금까지 제시한 문헌들을 종합해보면은 시장효율성과 관련된 연구와 추적오차 그리고 제도에 관련된 연구들이 존재하는데, 시장효율성과 관련된 연구의 경우, ETF의 운용과 관련된 연구라고 보기는 어렵고, ETF의 운용과 관련 있는 추적오차의 연구들은 제도적 제약보다는 대부분 경제적 변수와 관련된 연구로서 존재하고 있다.9) 또한, 제도와 관련된 연구도 과세제도나 소비자보호 측면의 연구결과들이며, ETF를 운용하는데 있어서 법적제약이 ETF의 운용 결과에 미치는 영향을 실증분석한 연구는 아니다. 그래서 현재 펀드를 운용하는데 있어서 법적인 제약사항이 펀드성과에 영향을 미칠 수 있는 가능성이 있음에도 불구하고, 이러한 연구가 아직 활발하지 않은 상황인데, 이러한 부분은 법률적인 측면이 금융시장에 미치는 영향을 확인하는 연구로서 시도해 볼 필요가 있는 연구다. 부연하면 지수나 선물지수를 추종 혹은 그 2배를 추종하는 ETF의 경우 해당 상품 자체를 투자하는 측면에서 이용될 수도 있겠지만 이미 투자된 다른 자산에 대해 위험을 헷지하는 측면이나 무위험 차익거래 측면에서도 ETF를 이용할 수 있다. 즉, ETF를 헷지수단으로 이용하는 경우에 ETF의 추적오차가 높아지면 그만큼 ETF를 이용한 헷지의 정확성이 낮아질 소지가 있으며 현재 파생상품 비율을 제한하는 제도적인 상황이 추적오차에 영향을 줄 수 있고 추가적으로 헷지의 정확성에도 영향을 미칠 수 있다는 것이다. 또한, ETF를 차익거래 수단으로서 기초자산의 대용으로 이용되는 경우 무위험 차익거래 이론을 적용하더라도 추적오차로 인해 차익을 발생시키지 못할 가능성이 있으며 이러한 부분 역시 파생상품 비율을 제한하는 제도적 상항이 추적오차에 영향을 줄 수 있고 추가적으로 무위험 차익거래에도 영향을 줄 수 있어 파생상품 비율에 대한 추적오차의 실증연구를 시도할 필요가 있다. 따라서 본 연구에서는 레버리지 ETF를 운용하는데 있어 파생상품 사용제한이 ETF의 운용에 미치는 영향을 추적오차의 관점에서 실증분석 해보고자 한다. 그리고 실증분석을 토대로 시사점을 제시하고자 한다.
3. 연구가설 및 분석자료
3.1 연구가설
본 연구에서는 파생상품 운용제한과 관련하여 파생상품 위험평가액을 ETF의 순자산으로 나누어 비율로 계산하고, 이 비율이 추적오차에 영향이 있는지 확인해 볼 것이다. 먼저, 파생상품 위험평가액을 ETF의 순자산으로 나눈 값을 ‘파생상품 비율’로 정의 할 것이다. 그리고 이 비율이 100%로 제한되고 있을 당시에 운용되고 있었던 지수를 2배 추종하는 레버리지 ETF를 대상으로 파생상품 비율 완화의 필요성 여부를 분석할 것인데, 아래와 같이 가설을 제시해 볼 것이다.
가설 1: 파생상품 비율이 200%로 완화하기 전에 100%로 제한되어 운용되고 있는 지수를 2배 추종하는 레버리지 ETF의 추적오차는 파생상품 비율의 영향을 받는다.
첫 번째 가설은 파생상품 비율이 100%로 제한되고 있을 시기에 지수를 2배 추종하는 레버리지 ETF가 운용을 하는데 있어, 파생상품 비율이 레버리지 ETF 추적오차에 영향을 주는지 확인해 보고자 하는 가설이다. 만약에 이 가설이 기각 된다면, 당시에 파생상품 비율을 제도적으로 완화 시킬만한 필요성이 있다고 보기 어렵다고 할 수 있다. 하지만 반대로 이 가설을 기각 할 수 없다면, 파생상품 비율이 지수를 2배 추종하는 레버리지 ETF의 추적오차에 영향을 주고 있어, 파생상품 비율을 제도적으로 완화하는 것을 당시에 고려 볼 필요가 있다고 할 수 있다. 그리고 파생상품 비율이 100%에서 200%로 상향하여 제도적 완화가 되었지만 그 비율이 여전히 제한된 이후에 출시한 선물지수를 2배 추종하는 레버리지 ETF와 관련하여, 가설 1과 비슷하게 아래와 같이 추가로 가설을 제시해 볼 것이다.
가설 2: 파생상품 비율이 100%에서 200%로 완화하여 제한된 이후에 출시한 선물지수를 2배 추종하는 레버리지 ETF의 추적오차는 파생상품 비율의 영향을 받는다.
두 번째 가설의 경우, 파생상품 비율이 100%에서 200%로 상향되어 제도적인 완화 조치가 발생한 다음에 출시한 선물지수를 2배 추종하는 레버리지 ETF와 관련하여, 파생상품 비율이 추적오차에 영향을 미치는지 확인하는 가설이다. 여기서 선물지수를 2배 추종하는 레버리지 ETF의 경우, 포트폴리오 구성에 있어 지수를 2배 추종하는 레버리지 ETF와 다르다. 구체적으로 선물지수를 2배 추종하는 레버리지 ETF의 경우, 자산의 많은 비중을 선물계약으로 구성하고 있으며, 지수를 2배 추종하는 레버리지 ETF의 경우, 지수에 속한 주식들과 선물계약을 함께 구성하여, 결과적으로 선물지수를 2배 추종하는 레버리지 ETF와 지수를 2배 추종하는 레버리지 ETF는 포트폴리오 구성성격이 다르다. 즉, 지수를 2배 추종하는 레버리지 ETF의 2배 레버리지는 선물지수를 2배로 추종하는 것이 아닌 지수를 2배 추종하기 때문에 지수에 편입된 종목을 ETF의 포트폴리오로 구성하고 추가로 2배의 레버리지로 맞추기 위한 수단을 선물계약으로 이용한다. 하지만 선물지수를 2배 추종하는 레버리지 ETF의 경우 지수를 2배 추종하는 것이 아닌 선물지수 그 자체를 2배 추종하기 위해서 해당 지수를 구성하는 주식 종목들보다는 주로 선물계약을 통해 ETF의 포트폴리오를 구성하게 되는데 이때 지수를 2배 추종하는 레버리지 ETF보다 선물계약의 사용 정도가 더 높을 수 있다는 것이다.10), 따라서 지수를 2배 추종하는 레버리지 ETF와 비교하여 선물지수를 2배 추종하는 레버리지 ETF는 파생상품 사용이 포트폴리오 구성에 더 주요한 역할을 할 수 있다. 그리고 파생상품 비율이 지수를 2배 추종하는 레버리지 ETF와 선물지수를 2배 추종하는 레버리지 ETF에 상관없이 추적오차에 영향을 줄 수 있는 이유는 각 레버리지 ETF가 지수나 선물지수를 추종하되 그것을 그대로 추종하는 것이 아니라 2배로 추종해야 하는데 여기서 선물계약이 이용되기 때문이다. 즉, 선물계약의 경우 1계약 당 증거금만 있어도 거래가 가능하지만 1계약 거래금액 단위가 지수에 편입된 종목들과 비교해서 높기 때문에 파생상품 비율을 제한하면 레버리지를 정확히 맞추기 어렵고 이로 인해 추적오차가 발생할 수 있다. 예를 들어서 레버리지를 맞추기 위해 선물계약이 9계약에서 10계약 필요하다고 가정하고 9계약을 이용하면 파생상품 비율 제한을 넘지 않지만 레버리지가 정확하지 않을 수 있는 상황이며 10계약을 이용하면 파생상품 비율 제한은 넘지만 레버리지가 정확해질 수 있는 상황이라면 9계약을 이용해서 레버리지를 정확히 맞추지 못해 추적오차가 발생할 수 있다는 것이다.11), 그래서 결과적으로 이러한 부분으로 인해 파생상품 비율이 100%에서 200%로 완화하여 제한된 이후에 출시한 선물지수를 2배 추종하는 레버리지 ETF 추적오차에 영향을 미칠 수 있을 가능성이 있다. 따라서 가설 2를 통해 이러한 현상이 나타나는지 확인해 볼 것이다. 구체적으로 지금까지 언급한 가설 1과 가설 2를 통계적으로 검증하는데 있어 파생상품 비율에 대한 영향과 관련해 Hur et al.(2012)의 방법론을 레버리지 ETF 분석에 맞게 보완하여 아래와 같이 식을 제시할 것이다.
식 (1) 밑에 표시된 i는 종목을 의미하고 t는 시점을 의미하는데 TEi,t는 아래 식 (2)과 같이 ETF의 추적오차, 1nDRi,t는 식 (3)과 같이 파생상품 비율에 자연로그를 취한 값으로서 파생상품 비율을 그대로 적용할 경우 분포가 한쪽으로 쏠리는 현상을 감안하여 자연로그를 통해 변수를 변환해 사용한 것이다.12), 이 변수가 통계적으로 유의하다면 파생상품 비율이 추적오차에 영향을 받는다. CRit는 ETF 포트폴리오에서 현금이 차지하고 있는 비율인데 현금의 경우 KOSPI200 지수나 KOSPI200 선물지수에서 구성되지 않은 자산항목으로서 이러한 비율이 추적오차에 영향을 미칠 수 있어 통제변수로 사용했다. 1nNAVit는 Hur et al.(2012)의 연구에서와 같이 ETF 순자산가치에 자연로그 ln을 취한 값을 의미하여 순자산가치에 대한 크기가 추적오차에 영향을 미칠 수 있는 부분을 감안해 통제변수로 사용하였고 그 외에 다른 변수들은 아래와 같이 식 (4), 식 (5)로 계산했다.
이후에 표시된 Divdit 는 ETF의 분배금 비율로서 Hur et al.(2012)에 언급된 것과 같이 분배금 발생으로 인한 영향을 통제하였고, Mgnit는 선물계약의 증거금 비율로서 레버리지를 발생시키는 선물계약에 증거금에 따라 추적오차의 영향이 달라질 수 있는 부분을 통제하였다. Volit는 추종 지수의 변동성으로서 Kim(2018)의 연구는 ETF의 가격오차에 대한 통제변수로 사용했는데, 이러한 변동성이 추적오차에도 영향이 있을 수 있어 통제변수로 사용했다. 여기서 변동성의 경우 측정방식이 여러 방법론으로 존재하여, 아래 <표 2>와 같이 세분화해서 계산했다.
<표 2>를 확인해보면, 당일 변동성에 해당하는 장중최고가격과 장중최저가격을 반영한 계산방식, 확률변동성 모형인 GARCH 계열 방법으로 세분화하였다. 이것은 추적오차의 경우에 최근 기준을 통해 산출하므로, 과거정보가 반영되지 않은 당일에 측정된 최고지수와 최저지수를 이용해 계산한 변동성이나, 최근의 정보반영이 상대적으로 높고 과거의 정보반영이 상대적으로 낮은 GARCH 계열의 방식을 세분화하여 계산한 변동성으로 통제했다.13), 그리고 Matit의 경우 선물만기를 1년 기준 비율로 환산한 값으로 선물만기가 추적오차에 발생할 수 있는 영향을 통제하였다. 그래서 제시한 식 (1)에서 파생상품 비율인 1nDRit변수가 통계적으로 유의하게 나타난다면 추적오차인 TEit 변수에 영향을 미친다고 볼 수 있다. 따라서 가설 1과 가설 2에서 추적오차인 TEit 변수가 파생상품 비율인 1nDRit 변수에 통계적 유의성을 가지는지 여부로 가설의 기각 여부를 확인해 볼 것이다. 또한, 식 (1)을 분석하는데 있어 패널자료가 이용되었는데 패널자료의 경우 일반적인 Pooled OLS 방법을 통해 분석할 경우 문제점이 나타날 수 있다. 따라서 고정효과(Fixed Effect) 모형과 확률효과(Random Effect) 모형 중에서 Hausman(1978) 검정을 통해 선택하였다.14)
3.2 연구자료
본 연구에서는 2013년 1월 2일부터 2018년 6월 22일까지 분석기간을 설정하여 실증분석 했다. 분석에 필요한 ETF 관련 자료를 기본적으로 FNGuide에서 제공받았으며, 직접 제공되지 않는 추적오차, 파생상품 비율, 현금비율, 변동성 등의 변수값은 FNGuide에서 제공받은 자료를 통해 직접 계산하였고, 증거금은 한국거래소에 공지된 사항을 이용하였다.
분석대상 자료는 KOSPI200 지수나 KOSDAQ150 지수를 2배 추종하는 레버리지 ETF와 KOSPI200 선물지수, KOSDAQ150 선물지수를 의미하는 F-KOSDAQ150 지수를 2배 추종하는 선물레버리지 ETF로 설정했는데, 각 추종지수를 2배로 맞추는데 있어서 역으로 2배 추종하는 ETF도 분석대상에 포함했다. 그래서 본 연구에서 분석대상으로 설정한 ETF 상품들은 <표 1>에 정리하였다.
4. 분석결과
4.1 기초통계량 및 상관계수
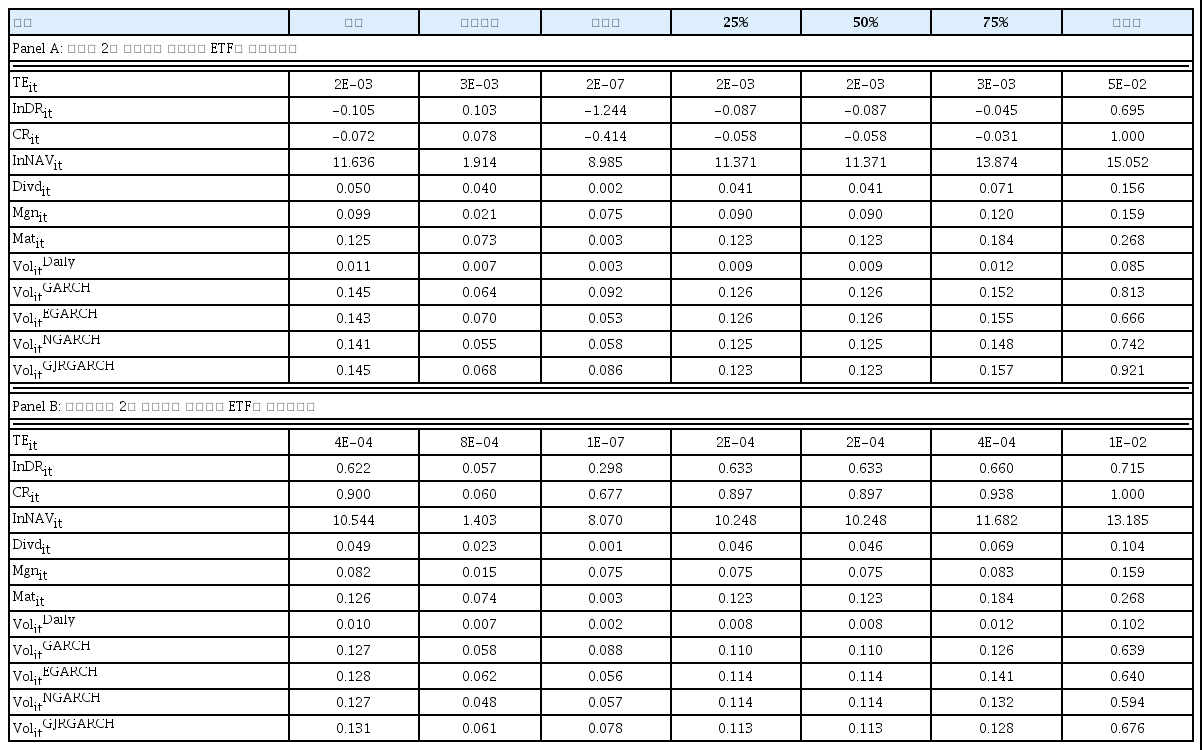
본 연구에서 분석할 자료의 기초통계량은 지수를 2배 추종하는 레버리지 ETF와 선물지수를 2배 추종하는 레버리지 ETF의 기초통계량으로 구분하여 <표 3>으로 정리했다.
기초통계량과 관련된 내용을 확인해보면, 파생상품 비율을 의미하는 1nDRit 변수는 지수를 2배 추종하는 레버리지 ETF에서는 -0.105의 평균, 선물지수를 2배 추종하는 레버리지 ETF 에서는 0.622의 평균을 가지는 것으로 나타났는데 이것은 exp함수를 통해 다시 파생상품 비율로 환산하면 각각 0.9, 1.86에 해당된다. 이것은 선물지수를 2배 추종하는 레버리지 ETF가 지수를 2배 추종하는 레버리지 ETF보다 높은 파생상품 비율을 가지고 있음을 알 수 있으며 두 레버리지 ETF의 포트폴리오 구성성격이 다를 수 있음을 함의하고 있다. 또한, 기초통계량을 통해 확인했을 때 ETF에 파생상품 보유한도를 위반하는 것으로 보이는 경우도 일부 발견되었다. 그리고 ETF 포트폴리오에서 현금이 차지하는 현금비율 CRit 변수의 경우 지수를 2배 추종하는 레버리지 ETF의 경우 -0.072의 평균, 선물지수를 2배 추종하는 레버리지 ETF에서는 0.90의 현금비율을 가지고 있으며 음의 평균을 가지고 있다는 것은 차입을 통해 포트폴리오를 구성하고 있음을 의미하는데 이 역시 지수를 2배 추종하는 레버리지 ETF와 선물지수를 2배 추종하는 레버리지 ETF의 포트폴리오 구성성격이 다르다는 것을 함의한다. 파생상품 증거금 비율을 나타내는 Mgnit 변수의 경우, 한국거래소에서 시장의 상황에 따라 요구하는 증거금을 조정하고 있는데, 지수를 2배 추종하는 레버리지 ETF에서는 0.099의 평균, 선물지수를 2배 추종하는 레버리지 ETF에서는 0.082의 평균을 가지고 있었다. 이것은 선물지수를 2배 추종하는 레버리지 ETF의 출시가 늦어서 나타난 차이라고 볼 수 있는데 평균값을 기준으로 봤을 때 과거보다 최근의 증거금 비율이 감소했음을 함의하고 있다. 그리고 이 증거금 비율을 통해 약 10배에서 12배정도의 레버리지를 가질 수 있고 보수적으로 두 레버리지 ETF의 최대값인 0.159 기준으로 약 6.3배의 레버리지로 나타나, 현재 2배로 제한되고 있는 레버리지 ETF보다 훨씬 더 높은 레버리지를 가지는 ETF도 설계가 가능하다는 것을 의미하고 있다.15), 그리고 변동성의 경우, GARCH 계열의 측정방식에서 평균기준으로 대부분 비슷한 값을 나타냈는데, 본 연구에서는 GARCH로 측정한 변동성 값이 0.01 미만으로 측정된 일부 값은 Kim and Kim(2017)의 연구에서와 같이 제외하였다.
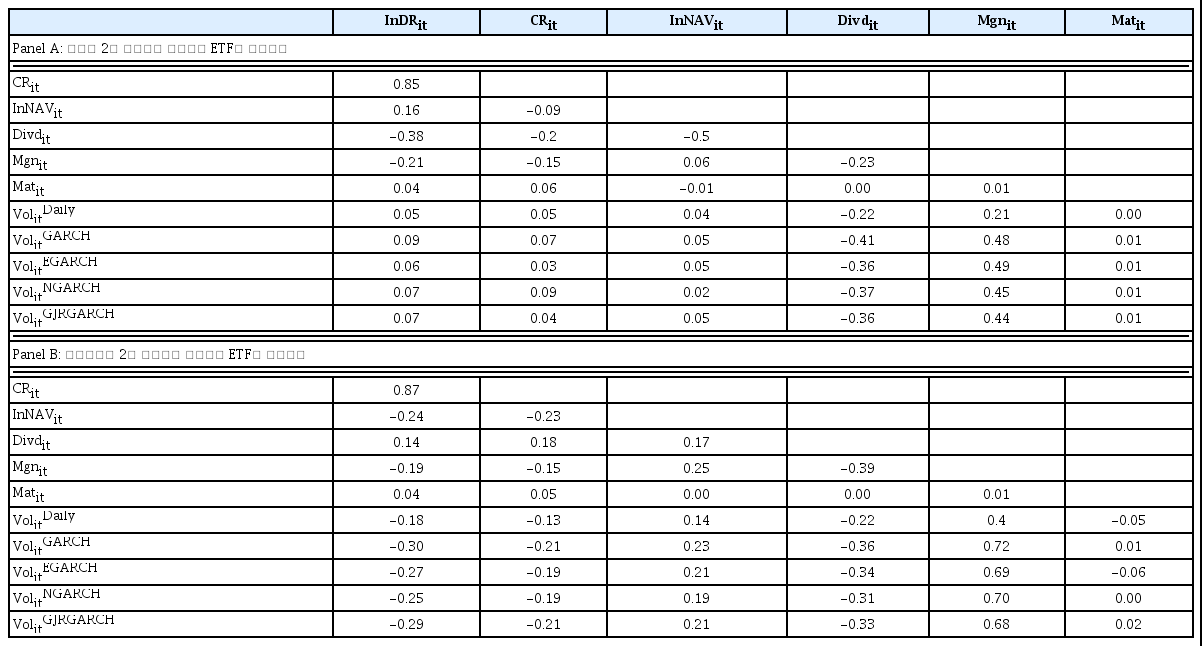
상관계수의 경우 <표 4>에 제시하였다. 결과를 확인해보면 지수를 2배 추종하는 레버리지 ETF와 선물지수를 2배 추종하는 레버리지 ETF에서 파생상품 비율과 현금비율의 상관계수가 높게 나타났다. 이 경우 회귀분석을 하는데 있어 다중공선성 문제가 존재하는지 추가로 확인해 볼 필요가 있는데 Marquaridt(1970)에서 언급된 VIF(Variance Inflation Factor) 분석을 통해 <표 5>와 같이 그 결과가 10을 넘지 않아 회귀분석에서 다중공선성의 문제가 되지 않음을 확인했다.16) 그 외에 회귀분석에 설정한 다른 변수들도 VIF 분석을 통해 다중공선성의 문제가 되지 않음을 확인했다.
4.2 가설 1, 가설 2 분석결과
가설 1의 경우, 파생상품 위험평가액을 ETF의 순자산으로 나눈 파생상품 비율이 100%로 제한된 경우에 지수를 2배 추종하는 레버리지 ETF와 관련된 가설이며, 가설 2의 경우, 파생상품 비율이 100%에서 200%로 완화하여 제한된 이후에 출시한 선물지수를 2배 추종하는 레버리지 ETF와 관련된 가설이다. 먼저, 가설 1에 대한 분석 결과를 <표 6>과 같이 정리하였다. 여기서 <표 6>의 세로축은 식 (1)의 독립변수를 의미하며, 여러 독립변수 중에서 변동성의 경우에 <표 2>와 같이 구분하여 제시하고, 가로축에 변동성에 해당하는 <표 2>의 번호를 부여했다. 그리고 각 변수에서 위에 표시된 숫자는 분석결과의 계수를 의미하고, 아래에 표시된 숫자는 분석결과의 t-통계값을 의미하며, 위에 표시된 *의 표시는 10%에서 통계적 유의, **의 표시는 5%에서 통계적 유의, ***의 표시는 1%에서 통계적 유의를 의미한다.
가설 1을 검정한 <표 6>의 Panel A를 확인해보면, 파생상품의 위험평가액을 ETF의 순자산으로 나눈 파생상품 비율 변수에 자연로그를 취한 1nDRit이 모든 결과에서 음의 계수값을 가지고 있었고 통계적으로 유의한 결과로 나타났다. 이것은 파생상품 비율이 지수를 2배 추종하는 레버리지의 ETF 당일 추적오차에 영향을 미친다는 의미로 해석 할 수 있으며 앞서 제시한 가설 1을 기각하기 어렵다고 볼 수 있다. 또한, 현금이 포트폴리오에 차지하는 비중을 나타내는 현금비율 변수인 CRit 변수가 양의 계수값을 가지면서 유의하게 나타났다. 이것은 현금비율의 높아지면 추적오차가 커진다는 의미를 가지고 있다. 그리고 지수를 2배 추종하는 레버리지 ETF에서 분배금을 나타내는 Divdit변수의 경우, 양의 계수값을 가지면서 유의하게 나타났는데 이것은 분배금이 발생하면 추적오차가 커진다는 의미를 가지고 있다. 그 외에 증거금을 의미하는변수는 유의성을 Mgnit 변수와 만기를 의미하는 Matit 변수는 양의 계수값을 가지면서 통계적으로 유의하게 나타났는데, 이것은 변동성이 커질수록 추적오차가 증가하는 관계와 만기가 길어질수록 추적오차가 커진다는 것을 의미한다.
종합해보면 파생상품 비율을 100%로 제한하고 있는 당시에 상황을 기준으로 봤을 때, 지수를 2배 추종하는 레버리지 ETF 운용에 제약이 될 수 있음을 확인했다. 따라서 당시에 파생상품 비율을 100%에서 200%로 상향하여 제한을 완화 할 필요성이 있다고 볼 수 있으며, 결과적으로 가설 1을 기각하기 어렵다. 그리고 파생상품비율이 당일 추적오차에 미치는 영향을 나타낸 식 (1)의 종속변수를 TEit 에서 TEit+1 로 바꾸어 익일 추적오차에 미치는 결과도 <표 6>에 Panel B로 제시하였다. 결과를 확인해보면 1nDRit 변수가 익일 추적오차에 영향을 미치는 것으로 나타났는데 결과적으로 가설 1을 기각하기 어렵다고 볼 수 있다.
이렇게 가설 1을 통해 파생상품 비율이 100%로 제한 되어있는 경우 파생상품 비율이 지수를 2배 추종하는 레버리지 ETF 추적오차에 영향을 줄 수 있음을 확인했는데 그렇다면 파생상품 비율이 100%에서 200%로 상향된 경우에도 여전히 파생상품 비율이 지수를 2배 추종하는 레버리지 ETF 추적오차에 영향이 있는지 확인해 볼 필요가 있다. 따라서 그러한 결과를 <표 7>에 제시하였다. <표 7>도 <표 6>에서와 같이 세로축은 식 (1)의 독립변수를 의미하며, 여러 독립변수 중에서 변동성의 경우에 <표 2>와 같이 구분하여 제시하고, 가로축에 변동성에 해당하는 <표 2>의 번호를 부여했다. 그리고 각 변수에서 위에 표시된 숫자는 분석결과의 계수를 의미하고, 아래에 표시된 숫자는 분석결과의 t-통계값을 의미하며, 위에 표시된 *의 표시는 10%에서 통계적 유의, **의 표시는 5%에서 통계적 유의, ***의 표시는 1%에서 통계적 유의를 의미한다.
<표 7>의 결과를 확인해보면 Panel A에서 파생상품 비율이 당일 추적오차에 미치는 영향과 관련해 1nDRit 변수가 통계적 유의성을 보이지 않았다. 또한 Panel B에서 파생상품 비율이 익일 추적오차에 미치는 영향과 관련해서도 1nDRit 변수가 통계적 유의성을 보이지 않았다. 이것은 파생상품 비율이 100%로 제한되는 제도적 상황에서 파생상품 비율이 지수를 2배 추종하는 레버리지 ETF 추적오차에 영향을 주지만 그 비율을 200%로 상향 조정하는 경우 이러한 현상이 나타나지 않게 된다는 것을 확인할 수 있다.17), 즉, 지수를 2배 추종하는 레버리지 ETF의 경우 지수에 해당되는 종목으로 포트폴리오를 구성하고 레버리지를 맞추는데 있어 선물계약을 사용할 때 파생상품 비율을 100%로 제한하는 경우 <표 6>과 같이 파생상품 비율이 추적오차에 영향을 미치고 있지만 100%에서 200%로 완화하는 경우 <표 7>과 같이 파생상품 비율이 추적오차에 영향을 미치지 않고 있음을 확인할 수 있다. 이러한 결과는 파생상품 비율의 제한을 완화함으로서 파생상품 비율에 대한 추적오차 영향이 통계적으로 유의하게 나타나지 않은 결과로 해석할 수 있다.
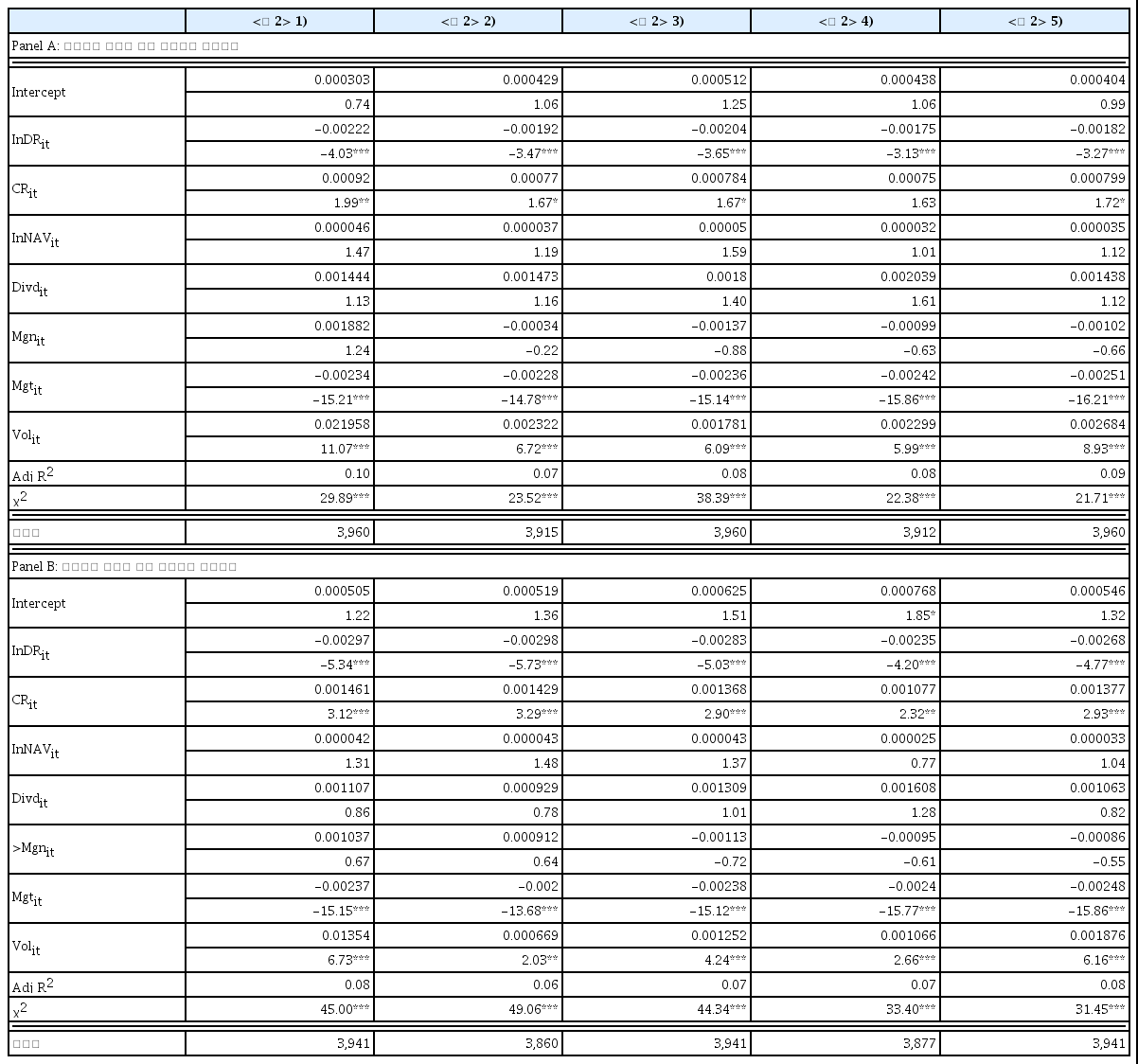
그렇다면 파생상품 비율이 100%에서 200%로 완화하여 제한된 이후에 출시한 선물지수를 2배 추종하는 레버리지 ETF에서도 같은 현상이 나타나는지에 대해 확인해 볼 필요가 있는데, 이것은 가설 2 통해 식 (1)로 분석하였으며, 그 결과를 <표 8>에 제시하였다. 여기서 <표 8>도 <표 6>과 <표 7>에서와 같이 세로축은 식 (1)의 독립변수를 의미하며, 여러 독립변수 중에서 변동성의 경우에 <표 2>와 같이 구분하여 제시하고, 가로축에 변동성에 해당하는 <표 2>의 번호를 부여했다. 그리고 각 변수에서 위에 표시된 숫자는 분석결과의 계수를 의미하고, 아래에 표시된 숫자는 분석결과의 t-통계값을 의미하며, 위에 표시된 *의 표시는 10%에서 통계적 유의, **의 표시는 5%에서 통계적 유의, ***의 표시는 1%에서 통계적 유의를 의미한다.

파생상품 비율이 200% 완화 이후 지수 레버리지 ETF의 분석결과
t-통계값 위에 표시된 *의 표시는 10%에서 통계적 유의, **의 표시는 5%에서 통계적 유의, ***의 표시는 1%에서 통계적 유의를 의미한다.
가설 2를 검정한 <표 8>을 확인해보면, Panel A의 경우 당일 추적오차에 대한 분석결과를 제시했는데 파생상품의 위험평가액을 ETF의 순자산으로 나눈 파생상품 비율 변수에 자연로그를 취한 1nDRit 변수가 모든 결과에서 음의 계수값을 가지면서 통계적으로 유의하게 나타났다. 이것은 선물지수를 2배 추종하는 레버리지 ETF의 경우, 파생상품 비율에 따라 추적오차가 달라질 수 있음을 함의하고 있다. 즉, 파생상품 비율이 선물지수를 2배 추종하는 레버리지 ETF 당일 추적오차에 영향을 미친다는 의미로 해석 할 수 있다. 그리고 다른 독립변수의 경우, 현금이 ETF 포트폴리오에 차지하는 비중을 의미하는 현금비율 CRit 변수에서 양의 계수값을 가지면서 통계적 유의성이 대부분 나타났고 1nNAVit 변수와 Divdit 변수 그리고 Mgnit 변수의 경우 통계적 유의성이 나타나지 않았다. 그리고 변동성 변수의 경우, 가설 1과 같게 모든 결과에서 양의 계수값을 가지면서 통계적으로 유의하게 나타나, 변동성이 커질수록 추적오차가 커지는 현상이 있는 것을 확인했다. 마지막으로 만기일을 의미하는 Mgtit 변수의 경우, 음의 계수값을 가지면서 통계적으로 유의하게 나타났다.18), 또한 파생상품비율이 당일 추적오차에 미치는 영향을 나타낸 식 (1)의 종속변수를 TEit에서 TEit+1로 바꾸어 익일 추적오차에 미치는 결과도 <표 8>에 Panel B로 제시하였다. 결과를 확인해보면 파생상품 비율에 자연로그를 취한 1nDRit 변수가 익일 추적오차에도 영향을 미치는 것으로 나타나 Panel A와 같이 Panel B에서도 1nDRit 변수에 대한 추적오차의 영향을 추가로 확인했다.19)
지금까지 분석한 자료의 경우 일별 자료를 이용해 파생상품 비율이 지수를 2배 추종하는 레버리지 ETF와 선물지수를 2배 추종하는 레버리지 ETF의 당일 추적오차와 익일 추적오차에 대한 영향을 분석한 결과인데 자료를 주간 평균으로 계산하여 분석한 경우에도 파생상품 비율에 자연로그를 취한 1nDRit 변수에 대한 추적오차의 영향을 확인해 강건성이 있음을 확인하였다. 구체적으로 파생상품 비율이 100%로 제한되는 경우 지수를 2배 추종하는 레버리지 ETF의 추적오차 분석에서 해당 주와 그 다음주의 추적오차에 영향이 있음을 확인하였고 100%에서 200%로 완화하여 제한된 이후에는 그러한 결과가 발생하지 않았다. 또한, 선물지수를 2배 추종하는 레버리지 ETF에서도 파생상품 비율이 해당 주의 추적오차와 그 다음 주의 추적오차에 영향이 미치는 것도 확인해 파생상품 비율에 대한 추적오차의 영향력을 추가로 확인하였다.20)
종합해보면 파생상품 비율을 100%에서 200%로 완화하여 제한된 이후에 출시한 선물지수를 2배 추종하는 레버리지 ETF의 경우, 파생상품 비율에 대한 영향이 추적오차에 나타나고 있다고 볼 수 있어, 가설 2를 기각 할 수 없었다.21) 즉, 파생상품 비율이 100%로 제한되는 시점에서 파생상품 비율이 지수를 2배 추종하는 레버리지 ETF의 추적오차에 영향을 미치는 것과 같이 파생상품 비율이 200%로 제한되는 현재 시점에서 파생상품 비율이 선물지수를 2배 추종하는 레버리지 ETF 추적오차에 영향이 있음을 확인했다.
4.3 가설 3 제시 및 분석결과
앞서 분석한 가설 2를 통해 선물지수를 2배 추종하는 레버리지 ETF의 추적오차는 파생상품 비율의 영향을 받는 것으로 나타났는데, 구체적으로 파생상품 비율이 증가하면 추적오차가 감소하고, 반대로 파생상품 비율이 감소하면 추적오차가 증가하는 음의 관계가 있다는 것이다. 즉, 파생상품 비율이 증가하여 추적오차가 감소되는 상황에서 파생상품 비율을 200%로 제한하면 추적오차를 감소하는데 영향이 있을 수도 있다는 것인데, 이러한 부분이 선물지수를 2배 추종하는 레버리지 ETF에 어떠한 영향이 있는지 추가로 확인해 볼 필요가 있다. 따라서 아래와 같이 추가로 가설 3을 제시하였다.
가설 3: 파생상품 비율의 200% 제한이 선물지수를 2배 추종하는 레버리지 ETF 추적오차에 영향을 미친다.
이 가설은 가설 2에서 파생상품 비율이 선물지수를 2배 추종하는 레버리지 ETF 추적오차에 주는 영향을 확장하여, 파생상품 비율을 제한하는 것이 추적오차에 영향을 주는지 확인하는 가설이다. 이러한 가설을 검정하기 위해서는 파생상품 비율이 200%에 가까운 상황과 그렇지 않은 상황의 자료를 구분하고 비교하여, 파생상품 비율이 200%에 가까운 자료의 추적오차가 그렇지 않은 자료의 추적오차보다 더 작은 추적오차를 가지게 되는지 여부를 통계분석으로 확인 할 수 있다. 그래서 가설 3의 수리적 가설을 식 (6)으로 제시하고, 이것에 대한 통계적 유의성을 확인하는 식 (7)을 통해 가설 3의 기각 여부를 확인해 볼 것이다.
식 (6)을 확인해보면, GroupA의 추적오차를 의미하는 TEGroupA평균이 GroupB의 추적오차를 의미하는 TEGroupB 평균과 비교해 더 높은 값을 가지고 있는 것으로 표현되고 있는데, 본 연구에서는 GroupB에 파생상품 비율이 200%에 가까운 자료로 설정할 것이고, GroupA에 그렇지 않은 자료로 설정할 것이다. 그래서 GroupB의 추적오차 평균인
분석결과를 확인해보면 <표 9> Group1에 파생상품 비율이 1.97 이상에서 1.99 미만을 가지는 표본과 <표 9> Group2에 파생상품 비율이 1.99 이상에서 2.01 미만을 가지는 표본을 비교한 결과의 경우, 평균값을 기준으로 <표 9> Group2가 <표 9> Group1보다 더 작은 값을 가지고 있었으며, 통계적으로도 유의한 결과를 보이고 있었다. 이것은 파생상품 비율이 200%에 가까운 경우에는 그렇지 않은 경우와 비교해 더 작은 추적오차를 가지는 것으로 해석할 수 있다. 즉, 파생상품 비율을 200%로 제한하는 상황에서 이 비율을 약간 위반하더라도 추적오차를 감소 시키는 운용에서 파생상품 비율을 200%에 가깝게 포트폴리오로 구성하는 것이 파생상품 비율을 200%보다 더 낮게 포트폴리오로 구성하는 것보다 더 좋은 결과로 나타난다는 것이다. 따라서 가설 3을 기각할 수 없었다.24), 또한, <표 9> Group3에 파생상품 비율이 2.01 이상에서 2.03 미만을 가지는 표본과 <표 9> Group2에 파생상품 비율이 1.99 이상에서 2.01 미만을 가지는 표본을 비교한 결과에서도 평균값을 기준으로 <표 9> Group2가 <표 9> Group3보다 더 작은 값을 가지고 있었으며, 통계적으로도 유의한 결과를 보이고 있었는데, 이러한 결과 역시 파생상품 비율이 200%에 가까울수록 추적오차가 감소하는 결과를 가져온다는 것이다. 즉, 파생상품 비율을 200%로 제한하지 않더라도 추적오차를 감소시키는 운용에서는 파생상품 비율이 200%에 가깝게 포트폴리오로 구성하는 것이 파생상품 비율을 200%보다 더 높게 포트폴리오로 구성하는 것보다 더 좋은 결과가 나타난다는 것이다. 이러한 결과는 선물을 2배 추종하는 레버리지 ETF의 운용금액이 높아질수록 추적오차에 의한 금액차이가 커질 수 있는데 만약 이러한 ETF를 이용해 헷지를 하는 경우 그 만큼 헷지에 대한 오차도 커질 수 있다. 예를 들어 운용금액이 100억 원인 경우 제시한 결과를 기준으로 하루에 약 180만 원의 헷지에 대한 오차가 발생할 수 있지만 운용금액이 1,000억 원인 경우 하루에 약 1,800만 원으로 헷지에 대한 오차가 발생해 운용금액이 높아질수록 추적오차에 의한 헷지 오차가 커질 수 있다. 또한, 이러한 오차가 시간이 지남에 따라 누적된다면 추적오차에 의한 헷지의 정확성이 보다 더 낮아질 수 있다. 한편으로 이러한 <표 9>의 결과를 확인 했을 때, 앞서 제시한 가설 2를 분석하기 위한 식 (1)에서 선형관계로 나타내 분석방법 외에 비선형적인 부분도 추가해 고려해 볼 필요가 있다. 즉, 식 (1)의 경우 추적오차의 원인을 파생상품 비율로 제시한 선형회귀분석 방식으로 결과로 <표 8>에 제시했지만 <표 9>결과는 추적오차가 파생상품 비율에 의해 감소했다가 다시 증가하는 U자형 형태를 나타나 비선형적인 부분도 있는지도 고려해 볼 필요가 있다는 것이다. 따라서 식 (1)에 파생상품 비율변수의 제곱한 값 변수로 추가하여 아래와 같이 식 (8)로 제시했다.25)
식 (8)의 경우 기존 식 (1)의 파생상품 비율의 제곱을 변수로 추가한 식으로 가설 3에서 제시된 <표 9>에 대하여 기존에 분석한 <표 8>에 대해 비선형적인 부분을 고려한 결과라고 할 수 있다. 그리고 그 결과를 <표 10>에 제시하였다.26)

가설 3 검정결과
가설 3에서 두 그룹의 차이가 통계적으로 유의한지 여부를 확인하는 결과로서 t-통계값 위에 표시된 *의 표시는 10%에서 통계적 유의, **의 표시는 5%에서 통계적 유의, ***의 표시는 1%에서 통계적 유의를 의미한다.
<표 10>의 결과를 확인해보면 Panel A의 당일 추적오차 분석결과에서 파생상품 비율변수가 음의 계수값을 가지면서 통계적으로 유의하게 나타나고 있다. 이것은 앞서 제시한 <표 8>의 분석결과와 마찬가지로 파생상품 비율에 대한 추적오차의 비선형적인 부분을 고려하더라도 파생상품 비율변수가 같은 방향의 계수값을 가지면서 통계적으로 유의하게 나타나고 있어 가설 2를 기각하기 어려운 상황이다.27), 다만, 익일 추적오차 분석결과인 Panel B와 관련하여 <표 8>의 경우 파생상품 비율변수가 유의하게 나타난 반면 <표 10>의 경우 t-통계값이 유의성에 미치는 정도가 없어지거나 약해지는 결과로 나타나 익일 추적오차에 대해서는 강건성이 있다고 보기는 어렵다. 결과적으로 당일 추적오차와 관련되어 가설 2를 기각하기 어렵다는 것을 다른 분석방법에 의해 추가로 확인할 수 있다.28), 또한, 파생상품 비율 제한이 추적오차에 영향을 미칠 수 있다는 부분을 확인하기 위해 파생상품 비율이 100%로 제한되는 시기와 200%로 제한되는 시기에 지수를 2배 추종하는 레버리지 ETF의 추적오차 크기를 <표 11>과 같이 제시했다.

가설 2에서 파생상품 비율의 비선형성을 고려한 검정결과
t-통계값 위에 표시된 *의 표시는 10%에서 통계적 유의, **의 표시는 5%에서 통계적 유의, ***의 표시는 1%에서 통계적 유의를 의미한다.

파생상품 비율 제한이 완화된 이후에 추적오차 감소의 검정결과
지수를 2배 추종하는 레버리지 ETF에서 파생상품 비율이 100%로 제한되는 추적오차 GroupA와 200%로 제한되는 GroupB를 비교한 결과로서 파생상품 비율이 200%로 제한되는 추적오차 GroupB가 더 낮은 추적오차의 평균을 가지면서 통계적으로 유의한 결과로 나타나고 있다. 여기서 t-통계값 위에 표시된 *의 표시는 10%에서 통계적 유의, **의 표시는 5%에서 통계적 유의, ***의 표시는 1%에서 통계적 유의를 의미한다.
<표 11>의 결과를 확인해보면 지수를 2배 추종하는 레버리지 ETF에서 파생상품 비율이 200%로 제한되는 시기의 추적오차가 파생상품 비율이 100%로 제한되는 시기의 추적오차보다 더 작은 추적오차의 평균을 가지고 있는 것을 확인할 수 있으며 통계적으로도 유의성을 가지고 있었다.29), 이것은 파생상품 비율의 제한이 완화되었을 때 추적오차가 작게 나타났다는 것을 의미하여 선물지수를 2배 추종하는 레버리지 ETF에서도 파생상품 비율 제한을 완화 할 경우 그 추적오차가 적어질 가능성이 있다.30)
가설 3의 결과를 정리하면, 파생상품 비율을 200%에 가깝게 설정하는 운용이 200%보다 더 낮게 설정하거나 반대로 더 높게 설정하는 것보다 결과적으로 더 낮은 추적오차를 발생시키는 결과로 나타났는데, 이것은 파생상품 비율을 200%로 제한하는 것이 추적오차를 감소시키는 운용에 제약이 될 수 있음을 함의한다. 즉, 현재 파생상품 비율이 200%로 제한된 상황에서 가설 2를 기반으로 파생상품 비율 증가가 추적오차 감소에 영향을 미치고 있는데, 여기서 파생상품 비율을 약간 위반하더라도 200%에 가깝게 포트폴리오를 구성하면 파생상품 비율을 200%보다 더 낮게 포트폴리오로 구성하는 것보다 더 낮은 추적오차를 가지게 된다는 것이다. 그래서 선물지수를 2배 추종하는 레버리지 ETF를 운용하는 입장에서 파생상품 비율을 200%로 제한하면 이것은 운용상 제약이 될 수 있음을 의미한다. 다른 한편으로 파생상품 비율이 200%에 가깝게 포트폴리오를 구성하는 것과 200%보다 더 높은 비율로 포트폴리오를 구성하는 것을 비교해, 오히려 200%보다 더 높은 비율을 가지는 포트폴리오의 추적오차가 커지는 상황이 발생했다. 또한, 파생상품 비율이 100%에서 200%로 제한을 완화한 이후에 지수를 2배 추종하는 레버리지 ETF의 추적오차를 비교한 결과, 파생상품 비율이 100%로 제한되는 시기보다 200%로 제한을 완화한 시기의 추적오차가 더 작게 나타났다. 이러한 결과는 파생상품 비율을 예전에 100%에서 200%로 상향된 것과 같이 200%에서 300%까지 크게 상향조정 해야 하지는 않더라도 현재 200%로 제한되어 있는 그 자체가 선물지수를 2배 추종하는 레버리지 ETF의 추적오차에 영향을 미칠 수 있어 이러한 부분을 제도적으로 개선 할 필요성이 있음을 시사한다. 즉, 이것은 선물지수를 2배 추종하는 레버리지 ETF를 운용하는 입장에서 파생상품 비율을 200%로 제한하지 않더라도, 추적오차를 감소시키는 운용을 위해 이 비율을 과도하게 넘기지 않게 운용을 할 것으로 보여, 결과적으로 현재 파생상품 비율이 200%로 제한되어 있는 제도적 제약에 대해 개선을 논의해 볼 필요가 있다.
예를 들어 분석결과를 기준으로 파생상품 비율이 203%가 넘어가면 추적오차가 다시 증가 할 가능성이 있는데 정책적으로 선물지수를 2배 추종하는 레버리지 ETF 운용에서 파생상품 비율을 205%나 210%로 일부 완화하는 것도 방법이 될 수 있다. 이 정도 수준에서 제약을 완화 한다면 ETF를 운용하는 입장에서 이전 보다 운용에 자율성을 가질 수 있고 정책을 결정하는 당국도 과도한 완화로 인해 높은 레버리지를 추종하는 ETF 출시의 우려도 없게 될 것이다. 이러한 방법 외에 정책을 결정하는 당국에서 다른 방법도 고려해 볼 수 있다.
5. 결론
본 연구에서는 레버리지 ETF 운용에 있어 관련된 제도적 상황이 운용결과에 어떠한 영향을 미치는지에 대해서 연구해보고자 시작하였다. 그리고 본 연구를 통해 크게 세 가지 결론을 도출하였다.
첫째, 파생상품 위험평가액을 ETF의 순자산으로 나눈 파생상품 비율이 100%로 제한되고 있을 당시에 거래되고 있었던 지수를 2배 추종하는 레버리지 ETF는 파생상품 비율에 추적오차가 영향을 받고 있음을 확인했다. 즉, 당시의 상황에서 파생상품 비율이 추적오차를 감소시키는 운용상 제약이 있다고 볼 수 있으며, 결과적으로 당시에 지수를 2배 추종하는 레버리지 ETF에서 파생상품 비율을 100%에서 200%로 상향하여 제도적으로 제한을 완화해야 할 필요성이 있었다고 볼 수 있다. 또한, 파생상품 비율이 100%에서 200%로 상향조정된 이후에 지수를 2배 추종하는 레버리지 ETF에서 파생상품 비율이 추적오차에 영향을 미치지 않음을 확인해 100%의 파생상품 비율로 제한된 당시의 제도적 제약에 추적오차가 영향을 받고 있음을 확인할 수 있었다. 즉, 이러한 결과는 파생상품 비율의 제한을 완화함으로서 파생상품 비율에 대한 추적오차 영향이 통계적으로 유의하게 나타나지 않은 결과로 해석 할 수 있다.
둘째, 파생상품 비율을 100%에서 200%로 완화하여 제한된 이후에 출시한 선물지수를 2배 추종하는 레버리지 ETF의 경우, 파생상품 비율이 당일 추적오차에 영향을 주고 있었다.
셋째, 파생상품 비율이 200%로 제한된 상황은 선물지수를 2배 추종하는 레버리지 ETF 추적오차를 줄이는데 제약이 될 수 있다. 구체적으로 파생상품 비율이 200%에 가까운 자료와 200%보다 더 낮은 자료를 비교 했을 때, 파생상품 비율이 200%에 가까운 자료의 추적오차가 더 작게 나타났다. 그리고 파생상품 비율이 200%에 가까운 자료와 200%보다 더 높은 자료를 비교 했을 때도 파생상품 비율이 200%에 가까운 자료의 추적오차가 더 작게 나타났다. 즉, 이것은 파생상품 비율의 200% 제한을 약간 초과하더라도 200%에 가깝게 설정하는 것이 그렇지 않은 자료와 비교해서 추적오차가 더 낮게 나타났다는 것이다. 따라서 파생상품 비율 제한을 일부 완화하면 추적오차가 감소될 가능성이 있다. 또한 가설 3의 분석결과와 관련해 가설 2에 대해 비선형적인 부분을 감안하여 분석한 결과에서 가설 2를 기각하기 어렵다는 것을 확인했다. 그리고 파생상품 비율이 100%로 제한되는 시기와 200%로 제한되는 시기의 지수를 2배 추종하는 레버리지 ETF 추적오차를 비교한 결과 파생상품 비율이 200%로 제한되는 시기의 추적오차가 100%로 제한되는 시기의 추적오차보다 평균적으로 작게 나타났다.
이러한 결과들을 종합했을 때 운용과 관련한 법률적 제한이 운용의 목표를 달성하는데 제약이 될 수 있음을 시사하고 있다. 즉, 파생상품 비율이 증가하면 선물지수를 2배 추종하는 레버리지 ETF의 추적오차가 줄어드는 상황에서, 파생상품 비율의 200% 제한을 약간 초과하더라도 200%에 가깝게 구성하는 것이 파생상품 비율을 200%보다 더 낮게 구성하는 것보다 더 낮은 추적오차를 가지고 있어, 파생상품 비율을 200%로 제한하는 것이 운용상 제약이 될 수 있다는 것이다. 다른 한편으로 파생상품 비율이 200%에 가까운 경우와 200%보다 더 높은 경우를 비교한 경우, 파생상품 비율을 200%보다 더 높은 경우의 추적오차가 더 높게 나타났다. 또한, 파생상품 비율을 제도적으로 완화한 경우 파생상품 비율이 지수를 2배 추종하는 레버리지 ETF 추적오차에 영향을 미치지 않게 되었다는 부분과 추적오차 자체도 감소했다는 부분도 확인되어 선물지수를 2배 추종하는 레버리지 ETF도 파생상품 비율을 완화 할 경우 추적오차 감소에 영향을 미칠 수 있다는 것이다. 그래서 파생상품 비율을 과거에 100%에서 200%로 상향조정한 것과 같이 현재 200%에서 300%까지 추가로 크게 상향조정 해야 하지는 않더라도 현재 파생상품 비율 제한이 200%인 자체가 추적오차에 영향을 줄 수 있어 이러한 부분을 제도적으로 개선할 필요가 있다는 것이다. 즉, 선물지수를 2배 추종하는 레버리지 ETF를 운용하는 입장에서 제도적으로 파생상품 비율을 200%로 제한하지 않더라도, 추적오차 감소를 위해 파생상품 비율을 과도하게 높이는 것은 지양 할 것으로 보여, 현재 파생상품 비율이 명목상 200%로 제한되어 있는 제도적 제약에 대해 개선을 논의해 볼 필요가 있다. 다만, 이렇게 파생상품 위험평가액을 비율로서 제한하는 제도를 추가로 개선하는 부분에 있어 재무금융의 관점에서 확인되지 않은 법률적인 관점의 논의도 필요해 보여, 법학 관련 연구에서도 이러한 문제가 추가로 다루어지길 기대한다.
References
Notes
2배 이상의 레버리지 ETF도 기술적으로는 가능할 수 있으나, 제도적으로는 현재 불가능하다.
레버리지 ETF 상품에 따라 역으로 2배의 성과를 나타내도록 설계된 펀드들도 존재한다.
파생상품 위험평가액은 Kim and Park(2005)에 의하면 거래금액을 기준으로 산정되는데, 각 ETF 포트폴리오의 선물계약수가 상황에 따라 계속 조정될 수 있고, 일일정산 한다는 점에서 실질적으로는 현재 선물지수에 거래 승수를 곱한 개념이라고 볼 수도 있다.
앞서 레버리지 ETF 정의에서 언급한 두 연구 외에 현재 레버리지 ETF 관련 연구는 Cho(2013), Kim et al.(2015)가 존재하고 있는데, 다른 ETF 관련 연구에 비하면 레버리지 ETF 관련 연구 자체가 많지 않은 상황이다.
시장효율성과 관련된 연구 이외에도 변동성과 관련한 Kong and Park(2012), 헷지와 관련된 Byun (2014), 수익률분포나 수수료 대비 이익을 연구한 Eom and Park(2014), Woo and Choe(2012), 경제상황과 관련한 Kim et al.(2015)의 연구도 존재하나 이러한 연구들 역시 ETF 운용제약과 관련된 연구라고 보기는 어렵다.
Chung(2012)의 경우, 추종지수의 변화와 ETF의 변화 차이를 그대로 계산하는 방법을 추적오차로 정의했는데, 이것은 추종지수와 ETF를 비교해 더 높은 성과를 나타내는지 여부를 확인하는 측도의 의미가 있어 초과성과를 측정하는 방법으로 볼 수 있다. 하지만 만약 ETF 운용에 있어서 초과성과에 목표를 두게 되면, Hur et al.(2012)에서 정의한 추적오차 최소화에 지장을 줄 소지가 있다.
실제 ETF 관련 상품설명서들을 살펴보면 추적오차는 순자산가치의 변화와 추종지수의 변화에 대한 차이를 기준으로 하고 있다.
Lee(2012)의 경우, ETF 법적 규제와 관련하여 레버리지 ETF와 관련한 언급은 있지만, 운용제약과 관련된 연구는 아니며, 일반투자자에 대한 보호측면의 의견을 언급하고 있다. 또한, 이 연구의 경우, 실증분석이 포함된 재무금융 관련 연구가 아닌 법학과 관련한 연구이다.
Elton el al.(2002)의 연구의 경우, 분배금과 관련한 계정이 분리된 제도적인 부분으로 추적오차를 언급하고는 있지만, 이것은 펀드를 운용하는데 있어서 제약사항이라고 보기는 어렵다.
실제로 본 연구의 기초통계량에서 파생상품 비율의 변수가 선물지수를 2배 추종하는 레버리지 ETF의 평균이 지수를 2배 추종하는 레버리지 ETF의 평균보다 높게 표시되고 있다.
본 연구에서 분석기간 동안 선물지수를 2배 추종하는 레버리지 ETF의 선물계약수가 평균적으로 15계약이며 이 정도 계약이면 1계약의 차이가 추적오차에 영향을 미칠 가능성이 높다. 다만, 이러한 부분과 관련하여 자세한 분석은 추후 다른 연구에서 진행되길 기대한다.
식 (2)에서 아래첨자가 NAV로 표시되면 ETF의 순자산가치의 일일변화율, BM이면 추종지수의 일일변화율 개념이다. 또한, 각 식에 NAV 표시는 ETF의 순자산 총액이다.
GARCH계열의 모형은 Bollerslev(1986) GARCH 모형, Nelson(1991)의 EGARCH 모형, Engle and Ng(1993)의 NGARCH모형, Glosten et al.(1993)의 GJRGARCH 모형을 사용하였는데 GARH 모형의 비교와 관련해서는 Kang and Ryu(2009)의 연구를 참고하길 바란다.
Hausman(1978) 검정을 통해 통계값이 유의성이 있으면 고정효과 모형을 사용하고 그렇지 않은 경우 확률효과 모형을 사용하였다.
다만, 이러한 레버리지 ETF 출시는 시장의 위험성 및 제도적인 부분과 관련하여 추가적인 논의가 필요할 수 있다.
상관계수가 높아 다중공선성이 우려되는 경우에 VIF분석과 관련해서는 Kim and Cho(2006)과 Choi et al.(2012)의 연구를 참고하길 바란다.
유익한 조언을 해주신 익명의 심사위원님께 감사드립니다.
이 결과는 앞서 분석한 가설 1의 결과와 상이한데 지수를 2배 추종하는 레버리지 ETF의 경우, 선물지수와 지수 사이에 베이시스로 인해 만기가 길어질수록 추적오차가 커질 가능성이 있으며, 선물지수를 2배 추종하는 레버리지 ETF의 경우, 선물만기가 지수선물, 개별주식선물, 지수옵션, 개별주식옵션의 만기일과 겹치는 부분으로 만기가 짧을수록 추적오차가 커질 가능성이 있다. 다만, 이러한 부분에 대한 구체적인 원인을 밝히는 것은 본 연구주제 범위를 벗어나므로 추후 다른 연구를 통해 실증되길 기대한다.
익일 추척오차 결과와 관련해서는 이후 추가분석 결과와 비교해 다시 논의한다.
추가로 분석해 볼 수 있는 방법론을 제시해주신 익명의 심사위원님께 감사드립니다.
여기서 만약 양측검정을 사용하게 될 경우 식 (6)에 제시한 연구가설의 두 변수가 같지 않음으로 제시되어야 하며 이것은 추적오차가 줄어드는지 여부를 확인하는 검정방법으로서 적절하지 않을 수 있다.
여기서 파생상품 비율은 앞서 분석한 회귀분석에서 파생상품 비율에 자연로그를 취한 ln〖DR_〖i t〗 〗의 형태가 아닌 DR_〖i t〗 의 형태이다.
양측검정의 연구가설 기각기준으로 살펴보았을 때 <표 9> Group1과 <표 9> Group2를 비교한 경우 10%의 유의수준에 있고 <표 9> Group2와 <표 9> Group3을 비교한의 경우 10%의 유의수준에는 있지 않지만 근접한 편이다. 결과적으로 파생상품 비율의 200% 제한이 선물지수를 2배 추종하는 레버리지 ETF 추적오차에 영향을 미친다는 가설 3과 관련해 <표 9> Group1과 <표 9> Group2를 비교한 결과를 가지고도 확인이 가능하며 이후에 제시되는 <표 11>에 대한 결과를 통해 가설 3을 기각하기 어렵다는 것을 확인할 수 있다. 또한, 양측검정으로 통계적 유의성을 판단하는 경우 <표 10>에서 제시한 비선형적인 요소를 고려하지 않아도 될 수 있다.
이러한 분석방법은 Jang and Jo(2017)의 연구를 참고하길 바란다.
식 (8)의 경우 파생상품 비율변수와 파생상품 비율의 제곱변수간의 다중공선성과 관련된 논의가 있을 수 있는데 Wooldridge(2012)에 의하면 이러한 형태의 비선형회귀식에서는 다중공선성에 대한 가정이 위배되지 않는다고 언급하고 있다.
표본에서 파생상품 비율이 200%를 넘은 경우가 없는 ETF 종목을 제외한 분석결과를 확인해도 제시한 가설 2의 결과를 부정하기 어렵다.
유익한 조언을 해주신 익명의 심사위원님께 감사드립니다.
양측검정 기준으로 1%의 유의수준에 있어 가설 3을 기각하기 어렵다는 것을 추가로 확인할 수 있다.
선물지수를 2배 추종하는 레버리지 ETF의 경우 파생상품 비율이 100%에서 200%로 상향되어 제한된 이후에 출시되어 파생상품 비율이 100%인 시기의 자료가 없어 추적오차 크기를 비교해 분석할 수는 없었지만 지수를 2배 추종하는 레버리지 ETF의 분석을 통해 선물지수를 2배 추종하는 레버리지 ETF에서도 파생상품 비율 완화로 추적오차를 감소시킬 수 있는 가능성이 존재한다.